CIS677: Outline for lecture 1
CIS677: Outline for lecture 1
(These are mainly just some notes for me, as I think about what to say;
you may find them useful adjuncts to your own notes. I'd be happy to
hear of areas that particularly need clarification.)
Computational geometry
The study of algorithmic problems in a geometric setting.
As a field, a product of its history. Generally:
- low dimensional
- "flat": not curves and surfaces.
- concerned with worst-case asymptotic complexity.
These limitations get weaker all the time.
I want to cover:
- fundamental problems: both of theoretical and engineering interest
- interesting algorithms:
- provably good algorithms with conceivable engineering interest, or
- algorithms that are pretty good in practice, or
- both!
Why would "engineers" study this?
- build conceptual vocabulary
- add to cost measures, algorithmic approaches, intuition.
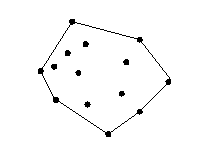
Convex hulls
Roughly:
- given some points in the plane,
- put some nails down at them.
- Surround the nails by a big rubber band, and let it shrink.
- The polygon enclosed by the rubber band is the convex hull
of the points.
What 2d convex hulls are good for:
- inside/outside, bounding shapes
- filtering: important points for these problems are vertices
- diameter of point set
- width
- smallest enclosing circle
- feasibility sets for linear programming
- "convex hull property" for some spline representations
- fun fact:
- the hull of the complex zeros of the polynomial p[x]
contains the hull of the zeros of its derivative.
Convex hulls, more formally
- convex combinations
- for points a,b, the point q is one if:
q is on the line segment between a and b, that is
q = za + (1-z)b for some z with 0<=z<=1
- convex set P:
-
closed under convex combination
if a,b in P, so is their convex combination
- convex: the whole plane, the empty set, disks, halfplanes, points, line segments
- not convex: {draw picture}
- the intersection of two convex sets is convex.
- convex hull or convex closure of a set S:
-
the "smallest" convex set containing S, that is
the intersection of all convex sets containing S.
Let conv(S) denote the convex hull of S.
Parts of the boundary of the convex hull (in the plane)
- vertices
-
points in P that are not convex combinations of other points in P
that is, v is a vertex if v is not in the convex hull of S-{p}
Suppose there's one site with smallest x coordinate.
Is it a vertex?
- edges
-
an edge is a line segment between two vertices,
with all of P on one side of the line through the edge.
Computing convex hulls: Jarvis march
Given: point set S
Find: vertices and edges of hull
Call the points of S sites
Pick a horizontal line L below all points of S
translate L until it contains at least one point p==p0 of S
repeat:
rotate counterclockwise about p from L until a point p' is hit;
output edge (p,p');
set L to the line through p and p';
p <- p';
until p==p0;
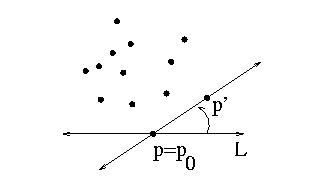
Does Jarvis march work?
- Facts:
-
each position of L has an associated halfplane containing conv(S);
each output edge on is the boundary of the hull;
no part of the boundary is missing;
Rotating about p from L
How do you do this, exactly?
One way: use polar angle about p from line to each site:
for unit vector v parallel to L,
find the max of
v dot (q-p)/||q-p||
among the sites q.
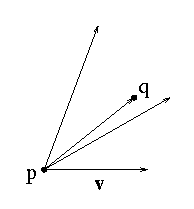
How long does Jarvis march take?
Suppose the number of output edges is A, the Answer size.
- Fact:
- A<=n, where S has n sites
Each time an edge is output, O(n) work is done.
So the total work is O(nA), or O(n2) in the worst case.
For some distributions of sites, A is expected O(log n),
so this algorithm is not so bad.
Computing convex hulls: incremental algorithms
The basic idea:
Add sites one by one, maintaining the hull.
That is, number the sites
p1 up to pn,
and maintain a set
Si=={p1, p2,...,pi},
and the convex hull of Si.
What happens when a site is added? Either
- the site pi is inside conv(Si-1), or
- the site pi is a vertex of conv(Si),
edges of the old hull are eliminated,
and new edges, incident to pi, appear
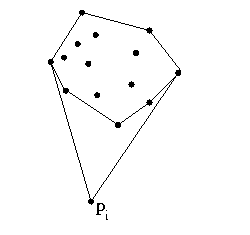
How can we tell which is true?
Testing if a site is a vertex
Suppose p is a site, and T is a set of sites. How is conv(T) related
to conv(p union T)?
Fact:
If p is not in conv(T), there is a line L that separates p and T.
Proof: use the fact that halfplanes are convex.
(Finding such a separating line is a linear programming problem.)
Fact:
If p is not in conv(T), there is a
line L through a hull edge that separates p and T.
Say that such an edge e is seen by p.
Facts
- an edge is deleted (not bounding conv(p union T))
if and only if it is seen by p
- (p, p') is a new edge if and only if p' is incident to an
unseen edge and a seen edge.
An incremental algorithm
Maintain a doubly, circularly linked list of vertices:
pairs of consecutive vertices give the edges.
Initialize with the triangle p1p2p3.
for i=4 to n,
find all edges of conv(Si-1) seen by pi;
delete these edges;
add new edges with pi as endpoint;
Two costs:
- Search: finding edges seen by p
- Update: deleting visible (seen) edges and adding new ones.
Update Cost
How much does it cost to delete edges and add new ones,
over the whole algorithm for computing conv(S)?
A given vertex may cause many edges to be deleted, however
at most 2 edges are created at each step,
and so: the total work for updating is O(n).
(A small-scale instance of amortized analysis
Search cost
One approach to search:
examine each edge for visibility
The search cost at step i is O(i), giving O(n2) work overall.
The expected work may not be so bad.
Speeding up search
It's possible to avoid looking at all the edges at each step.
Remark.
If one edge seen by p is known,
the rest are easily found, because:
Fact
The edges seen by pi are connected.
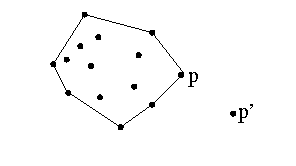
Fact:
Given a finite set T,
and point p in T that has the largest x-coordinate.
Suppose p' has larger x-coordinate than p.
Then
an edge incident to p is visible to p'.
An O(n log n) algorithm
Sort the sites by x-coordinate,
so pi <= pj if i < j.
do the incremental algorithm.
When adding pi, check edges starting with
those incident to pi-1.
Walk edges, checking visibility.
The work is dominated by the sorting time.
The algorithm need not maintain a doubly-linked list:
the upper and lower hulls can be maintained separately
as stacks.
Another approach to speeding up search
Pick a point o inside the convex hull;
As the incremental algorithm proceeds:
for each site p, keep track of the edge of the current hull crossed by the
line segment from o to p.
Call this edge crossed by p.
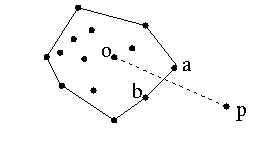
Here edge (a,b) is crossed by p.
This requires a pointer, for each site, and a list of sites,
for each edge.
Fact
The edge crossed by p is seen by p.
This solves the problem of finding an edge seen by p,
but makes another problem: what if the edge crossed by p is deleted?
Updating the crossed edges
If an edge crossed by p is deleted when pi is added,
one of the two new edges is crossed by p.
We need to know: how many different edges will be crossed by p,
in the course of the algorithm?
Randomization
Suppose the points pi are added in random order.
Lemma
For given site p and number i,
the probability that an edge crossed by p is incident
to pi is at most 2/i.
That is, the probability that an edge crossed by p is created
at step i is at most 2/i.
Or: the expected number of edges crossed by
p that are created at step i is at most 2/i.
Fact
The polygon conv(Si) is the same, no matter the ordering
of p1, p2,...,pi.
Proof of Lemma.
Suppose the edge crossed by p for conv(Si) is (a,b),
where a and b are two sites in Si.
The site a is equally likely to have been added at step 4,5,...i,
so the chance that a is pi is 1/i. The same is true for
b, and so
the probability that a or b is pi is 2/i.
Adding up the work for searching
Fact
The expected number of edges crossed by p, over the course of the
algorithm, is at most O(1)(1+1/2+1/3+1/4+...+1/n), or O(log n).
This uses the linearity of expectation, the fact
that the expected value of the sum of random variables is
the sum of the expected values.
That is, the expected work for searching, for a given site, is O(log n),
and the total expected work is O(n log n).
Remarks for the randomized incremental algorithm
Many other geometric problems are amenable to this approach.
This algorithm can be tweaked to be online, so
that a site does not need to be known before it is added.
If the sites are all vertices, then the algorithm is very close
to building a random binary search tree.
The expected running time is O(n) when the expected number of
vertices of a random subset of size i is O(i/log i).
Algorithms Galore
This does not exhaust the techniques that have been applied to
planar convex hulls. Some other approaches:
- Graham scan, which involves sorting by sites by their angle
about an interior point. The sorting based algorithm is roughly like this.
- divide-and-conquer: split the sites into equal-sized sets by a line,
compute the hulls of each set, and merge the results.
- algorithms that require O(n log A) in the worst case.
- algorithms that require n+o(n) expected work for random points.
- dynamic algorithms, that maintain the hull of a set from which
sites can be added and removed.
Degeneracy
Suppose, in the incremental algorithm,
a site lies on the line through an edge.
Should the site see the edge or not?
If always yes, some output edges may be collinear.
If always no, some output edges may be collinear.
Most algorithms have a special-purpose fix, that allows
degeneracies to be handled.
What if all sites lie on a line? Then there is no point in
the interior of the hull.
Primitives and robustness
Sometimes a reasonable implementation of the primitive test for
visibility can yield wildly wrong answers,
even for planar convex hulls.
The following is potentially part of the output for the
sorting-based algorithm:
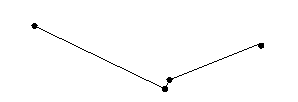
This interacts with solutions for handling degeneracy.
The moral is, that handling these issues is difficult, challenging,
and not necessarily boring.







