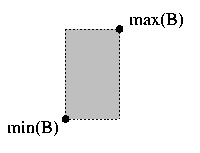CIS677: Notes for lecture 2, orthogonal range search and its relatives

CIS677
Notes for lecture 2:
Orthogonal Range Search and its Relatives


Coordinate-wise dominance and minima

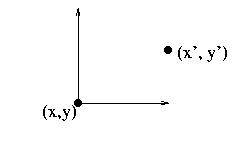
Definition: dominates
Say that point (x,y) dominates (x', y') if x<=x' and y<=y' and they're not equal.
example: comparison of towns for livability
Definition: minima
given point set S, minima of S have no dominators in S.
In the plane, minima are linearly ordered: listing in increasing x-order also gives decreasing y order.

relation to convex hulls:

Given point set S in the plane,
let S+- denote {(x,-y) | (x,y) in S}, define S-+ analogously, etc.
consider minima of S++, S+-, S--, S-+.
Fact:
if a point of S yields no minima in any of these four sets,
that point is not extreme in S (not a vertex of the convex hull)

computation of minima

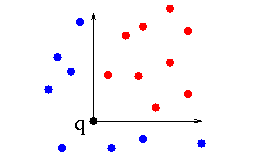
dominance queries

data:
set S of n points
query:
point q
output:
set of all p in S dominated by q

The set of points dominated by q is a box:

Definition: box
A box is a cross-product of intervals.
(also called rectangle, ortho-rectangle, rectilinear rectangle, rectagon)

A box has 2d sides in d dimensions, each side a box in d-1 dimensions.

Uses of dominance relation

testimony: use of minima in a networking problem

interval/interval or box/box intersections as dominance queries:

min(B).
For box B, let min(B) be the point of B dominating all others in B.
max(B)
The point of B dominated by all others in B.

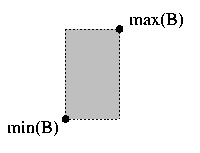
B and B' intersect iff:
min(B) dominated by max(B'), and
min(B') dominated by max(B),
or: (min(B), -max(B)) dominated by (max(B'), -min(B'))
It follows that a data structure for dominance queries can be used to for:

Box windowing

data:
set S of planar boxes
query:
planar box B, the window
output:
all boxes of S meeting B

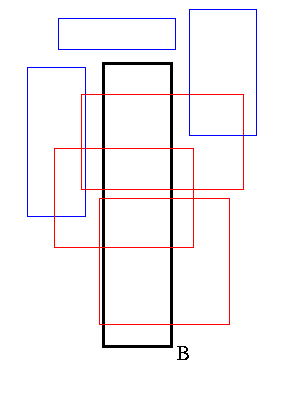
Dominance queries are a special case of:

Orthogonal range queries

data:
set S of n points
query:
box B
output:
set of all p in S and B

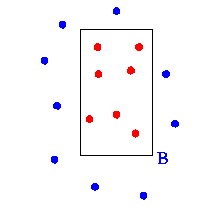
A box query in 2d can be answered by a dominance query in 4d.

First, consider:

1d range queries

Definition:

data:
set S of n values
query:
interval I=[a b]
output:
all p in S between a and b

one trivial solution for 1d queries: a sorted array of values in S.

for queries:
find smallest value in S > a using binary search
walk through array until greater than b.

This is O(A + log n) time solution;
It doesn't seem to generalize to 2d.

Range tree (binary tree) solution

Build a balanced binary tree for S to answer queries.

Some definitions:

S(m)
denotes the values stored in the subtree rooted at m;
split(m)
denotes the partioning value at m;
I(m)
denotes the interval (low(m) high(m)] containing S(m).
The subtree of the left child of m will store values in (low(m) split(m)]
The subtree of the right child of m will store values in (split(m) high(m)]

To answer a query I=[a b], traverse the tree, starting at root.

to visit a node m: 

	if m is a leaf, output the value point(m) if it is in I.
	otherwise:
		if I(m) meets I,
		then visit the children of m.

Query time O(A+log n):

To extend this to 2d, we need

Binary representation of intervals

Suppose I(m) is contained in I, but I(parent(m)) is not.
There are O(log n) such nodes m,
and the union of such intervals is I (when I has endpoints in S).
This is a "binary" or "canonical" representation of I.

If the S={0..2k-1}, and I=[0 b], then
(with suitable def. of median)
the intervals can be read off from the binary represention of b.

If we store S(m) at m, then I can be output as the union of O(log n) such sets.

Now consider

2d range queries

data:
set S of n planar points
query:
box B=[xl xh] X [yl yh]
output:
all p in S and B

In the 2d case, the binary representation
allows fast answering of "slab" queries,
with box B=[xl xh] X [-inf, +inf],
by building tree for x-coordinates of points of S.

For a node m in the tree,
S(m) becomes the set of points in a vertical slab.

2d Range trees

For fast 2d range queries,
for each node m of the tree,
build a "secondary" tree using y coordinates of points in S(m).

Find all nodes in primary tree for binary representation of [xl xh]
for each such node, use its secondary tree to find points with y-coordinates in [yl yh].

Query time:

O(Am + log n) for each node m of primary tree, where Am is output for m;
so O(A + log2 n) time altogether.

Space

O(n log n), since each point of S appears in O(log n) secondary trees.

Higher dimensional orthogonal range queries

data:
point set S in Rd
query:
box B=[xl xh] X [yl yh] X ...
output:
all points in B and S
solution:
build primary tree on x;
for each node, build structure for (d-1)-dimensional case.

Bounds:
O(n logd-1 n) space and O(A+logd n) query time

OK but not great for small d and for box windowing.

Let's turn to a better solution for:

Box windowing

data:
set S of planar boxes
query:
planar box B, the window
output:
all boxes of S meeting B

A given box B' in S either contains B, or one of its bounding segments has an endpoint in B, or has a bounding segment that crosses B.

We ignore the first possibility for now.

Consider short segments, with an endpoint in B, and
crossing segments, that cross B.

A 2d orthogonal range query data structure can report short segments.

A crossing segment must cross a left or bottom bounding edge of B. We need a:

Crossing segment data structure

data:
horizontal segments H
query:
vertical segment v
output:
segments in H crossed by v
The problem of reporting vertical crossing segments is solved the same data structure, rotated 90 degrees.

This problem leads to

Interval trees

1d case of crossing segment problem:

data:
intervals S
query:
value q
output:
all intervals in S containing q
This can be solved by dominance range query data structure in higher dimension, but this is more expensive than necessary.

Interval trees:

build a balanced tree on the 2n endpoints of S
at a given node m, store
straddle(m), theintervals of S containing split(m).

To answer a query:

follow search path in tree for q;
at a given node m on path, check if intervals in straddle(m) contain q.
To do this, build a data structure on straddle(m).

straddle sets

the condition that the intervals contain split(m) is helpful for search.
like interval queries, but grounded:
want a in S with min(a) < q, or max(a) > q.
That is, build a 1d range query data structure for endpoints of straddle(m).
The "sorted array" solution is adequate.

extension to crossing segment data structure

An interval tree solves the problem for vertical line queries, but what about segments? Need to find segments in H that cross segment, not whole line.

For a vertical segment [x x] X [yl yh],
any straddle set member in answer has an endpoint in [-inf x] X [yl yh].

Instead of just an ordered list for straddle set,
could use a 2d orthogonal range query data structure built on the straddle
set endpoints.

The range queries are of a special, grounded form,
better solved with:

Priority search trees

Solves the grounded box range query problem:

data:
set S of points in the plane
query:
grounded box B = [xl xh] X [-inf yh]
output:
all values in S and B

The 1d case of a "grounded" query is just:

1d grounded query:

data:
values S
query:
value q
output:
all values in S <= q
As in straddle sets, could use an ordered list; alternatively, use:

Heap:

value at root must be lowest in set, but left and right subtrees are otherwise open.

Priority search tree

construction:

Each node m has a corresponding box B(m):
min y of B(m) >= min y of parent B(m')
vertical slab containing B(m') contains the union of slabs for children.

To answer an orthogonal range query for a grounded box B,
recursively visit the nodes of the PST;
For a given node m,
check if point(m) in B;
if B(m) meets B, visit the children of m.

Query time

The nodes whose x-intervals are not contained in that of B are the same as for range trees, O(log n) total.

If the x-interval of m' is contained in that of B, then m is visited

only if B(m') meets B,
only if min y of B(m') less than max y of B,
only if point(m') in B(m) and B,
only if point(m') is output,
so O(A) such nodes are visited.

Hence, the work for a query is O(A + log n).

Summarizing windowing queries for horizontal segments:

need range trees for short segments, whose endpoints are in window;
interval trees handle segments crossing window,
using priority search trees on straddle sets.

Windowing queries for general segments

The general segment problem:

data:
set S of noncrossing line segments in the plane
query:
box B
output:
all segments in S meeting B

One approach to this problem is to use the bounding boxes of the segments in S, and answer box queries for those bounding boxes.

In typical situations, the set of segments with bounding boxes meeting B is a small superset of the correct output: the boxes allow "filtering" down to a small superset of the output.

But not in the worst case!

Another solution to this problem uses:

Segment trees

Given a set S of intervals,
store its 2n endpoints in a binary tree
store each interval I at a node m if:

that is, store I at nodes yielding its binary representation.
I stored at some of the nodes that would be visited
for I as a query in range search on the tree.
Storage is O(n log n)

As for box windowing,
use range queries for "short" segments;
crossing segments cross a boundary edge of the window.

window queries for crossing segments:

data:
set of non-intersecting segments
query:
window q
output:
segments that cross q

build a segment tree for x-projections of segments

The segments stored at a node
span the corresponding vertical slab.
build a 1D range tree for their intersection points with a vertical line:
any vertical line in the node's vertical slab meets the segments in the same order
this gives a total ordering of the segments,
and searching uses point/segment comparisons,
not value/value comparisons

To answer crossing segment queries,

for a vertical boundary edge: search segment tree for its projection
for each node on search path, use node's range tree to find
segments meeting edge

A few general tricks:

Filtering search

like interval trees, but even simpler and sometimes faster.
data:
set S of intervals
query:
point q
output:
all intervals in S containing q

The data structure is easily extended for the case where q is an interval.

The idea: partition the line into "apertures" (that is, intervals), such that:

  1. Any point in an aperture Z is in at least half the intervals meeting Z
  2. The total number of interval/aperture pairs that meet is O(n).

For each aperture, store a list of the sites that meet it. The storage is O(n) by (ii).

Given such a data structure, to answer a query:

find all apertures meeting q
for each such aperture, check each interval meeting it for containment of q.

There is an initial O(log n) cost to find the aperture containing q.

For each aperture, at least half the intervals meeting it will be output.

So, a query takes O(A + log n).

The discrete case: the endpoints of S and q are from some set of O(n) values.
Then initial search is O(1), and so O(A) overall.

The apertures act as "filters", giving a small superset of the output.

Finding the apertures

The algorithm finding the apertures is:

Sort the 2n endpoints of S,
and consider each one from left to right.
At any moment, an aperture is being grown to the right of some point.

maintain:

the current number C of intervals containing the current endpoint,
the minimum number Low of C over the current aperture,
T, the number of intervals meeting the current aperture.

Form a new aperture when Low becomes less than T/2, just before (i) is violated.