\( \newcommand\norm[1]{|| #1 ||} \newcommand\nnz[1]{{\textrm{nnz}(#1)}} \newcommand\E{\mathbf{E}} \newcommand\Dist{\mathbf{Dist}} \newcommand\reals{{\mathrm{I\!R}}} \newcommand\R{{\mathrm{I\!R}}} \newcommand\poly{{\textrm{poly}}} \newcommand\rank{{\textrm{rank}}} \newcommand\sr{{\textrm{sr}}} \newcommand\colspan{{\textrm{colspan}}} \newcommand\diam{{\textrm{diam}}} \newcommand\polylog{{\textrm{polylog}}} \newcommand\rowspan{{\textrm{rowspan}}} \newcommand\colbasis{{\textrm{colbasis}}} \newcommand\argmin{{\mathrm{argmin}}} \newcommand\Err{{\mathtt{NE}}} \newcommand\eps{{\epsilon}} \newcommand\bfone{{\mathbf{1}}} \newcommand\Var{{\mathbf{Var}}} \newcommand\stdev[1]{{\mathbf{stdev(#1)}}} \newcommand\cgf{{\mathbf{CGF}}} \newcommand\bfone{{\mathbb{1}}} \newcommand\Iden{{\mathbf{I}}} \newcommand\Prob{{\mathbf{Pr}}} \DeclareMathOperator\subg{\mathbf{subG}} \DeclareMathOperator\dist{\mathrm{dist}} \DeclareMathOperator\cost{\mathrm{cost}} \newcommand\cN{{\cal N}} \newcommand\cS{{\cal S}} \newcommand\cD{{\cal D}} \newcommand\cM{{\cal M}} \newcommand\cE{{\cal E}} \newcommand\cu{{\cal U}} \newcommand\cC{{\cal C}} \newcommand\KJL{K_{\mathbb{JL}}} \newcommand\tO{{\tilde O}} \newcommand\tL{{\tilde L}} \newcommand\maybemathbf[1]{\mathbf{#1}} \newcommand\matA{\maybemathbf{A}} \newcommand\matB{\maybemathbf{B}} \newcommand\matC{\maybemathbf{C}} \newcommand\matD{\maybemathbf{D}} \newcommand\matSigma{\maybemathbf{\Sigma}} \newcommand\matU{\maybemathbf{U}} \newcommand\matV{\maybemathbf{V}} \newcommand\matE{\maybemathbf{E}} \newcommand\matzero{\maybemathbf{0}} \newcommand\matW{\maybemathbf{W}} \newcommand\matZ{\maybemathbf{Z}} \newcommand\matY{\maybemathbf{Y}} \newcommand\matX{\maybemathbf{X}} \newcommand\matR{\maybemathbf{R}} \newcommand\matS{\maybemathbf{S}} \newcommand\matN{\maybemathbf{N}} \newcommand\matP{\maybemathbf{P}} \newcommand\vecx{\maybemathbf{x}} \newcommand\vecb{\maybemathbf{b}} \newcommand\hvecb{\hat{\maybemathbf{b}}} \newcommand\vecy{\maybemathbf{y}} \newcommand\tmatW{\tilde{\maybemathbf{W}}} \newcommand\tmatZ{\tilde{\maybemathbf{Z}}} \newcommand\tmatY{\tilde{\maybemathbf{Y}}} \newcommand\tmatX{\tilde{\maybemathbf{X}}} \newcommand\tvecx{\tilde{\maybemathbf{x}}} \newcommand\hmatS{{ \maybemathbf{\hat S}}} \newcommand\hmatR{{ \maybemathbf{\hat R}}} \newcommand\hmatA{{ \maybemathbf{\hat A}}} \newcommand\twomat[2]{\left[\begin{smallmatrix} #1 \\ #2 \end{smallmatrix} \right] } \newcommand\twomatr[2]{\left[\begin{smallmatrix} #1 & #2 \end{smallmatrix} \right] } \newcommand\tx{{\tilde{\mathbf{x}}}} \newcommand\tX{{\tilde{\mathbf{X}}}} \newcommand\tY{{\tilde{\mathbf{Y}}}} \newcommand\tA{{\tilde{\mathbf{A}}}} \newcommand\tW{{\tilde{\mathbf{W}}}} \newcommand\tZ{{\tilde{\mathbf{Z}}}} \newcommand\hS{{\hat {\mathbf{S}}}} \newcommand\hR{{\hat {\mathbf{R}}}} \newcommand\hA{{\hat {\mathbf{A}}}} \newcommand\hY{\hat {\mathbf{Y}}} \newcommand\bA{{\mathbf{A}}} \newcommand\bN{{\mathbf{N}}} \newcommand\ba{{\mathbf{a}}} \newcommand\bw{{\mathbf{w}}} \newcommand\W{{\mathbf{W}}} \newcommand\R{{\mathbf{R}}} \newcommand\bB{{\mathbf{B}}} \newcommand\bQ{{\mathbf{Q}}} \newcommand\bZ{{\mathbf{Z}}} \newcommand\bz{{\mathbf{z}}} \newcommand\bU{{\mathbf{U}}} \newcommand\bV{{\mathbf{V}}} \newcommand\bX{{\mathbf{X}}} \newcommand\bS{{\mathbf{S}}} \newcommand\bs{{\mathbf{s}}} \newcommand\bx{{\mathbf{x}}} \newcommand\by{{\mathbf{y}}} \newcommand\bb{{\mathbf{b}}} \newcommand\bT{{\mathbf{T}}} \newcommand\bP{{\mathbf{P}}} \newcommand\bG{{\mathbf{G}}} \newcommand\bY{{\mathbf{Y}}} \newcommand\bH{{\mathbf{H}}} \newcommand\bD{{\mathbf{D}}} \newcommand\be{{\mathbf{e}}} \newcommand\br{{\mathbf{r}}} \newcommand\Sig{{\mathbf{\Sigma}}} \newcommand\bLam{{\mathbf{\Lambda}}} \newcommand\bPi{{\mathbf{\Pi}}} \newcommand\hphi{{\hat\phi}} \newcommand\OPT{{\mathtt{OPT}}} \newcommand\sd{{\mathtt{sd}}} \)

Self-Improving Algorithms

`\qquad\quad`
Ken Clarkson


Joint with

Nir Ailon, Bernard Chazelle, Ding Liu, C. Seshadhri, Wolfgang Mulzer

IBM Almaden, Princeton Univ., both
(at the time, before 2013)

Machine Learning

Risk minimization The setup:
  • Training samples `z_1,z_2,\ldots`, where `z_k \sim \cD`
  • Concept space `C`
  • Loss function `\ell(c, z)\rightarrow \R^+` for `c\in C`, `z\sim\cD`
  • Risk of `c\in C` is `\E_{z\sim\cD}[\ell(c,z)]`

The goal: use samples `z_k` to approximately find `\argmin_{c\in C} \E_{z\sim\cD}[\ell(c,z)]`
For example, classification:
  • Also given: function `f(z)`
  • `C` is a set of functions on `z`
  • Loss `\ell(c,z)` is the expense if `c(z)\ne f(z)`

Here:
  • Also given: function `f(z)`
  • `C` is a set of algorithms with output `c(z) = f(z)`
  • Loss `\ell(c,z)` is the running time of algorithm `c` on `z`
So: for a given task and distribution over inputs, learn to run fast

Finding `\argmin`


Or at least, `\mathrm{arggood}`

  • Empirical risk minimization: minimize
    $$\sum_k \ell(c, z_k)\approx \E_\cD[\ell(c,z)]$$ can be helpful [GR16], but not always
    • May be too hard: no gradient in `C` space, etc.
    • Table lookup might win on training samples
  • Our strategy:
    • Find lower bound for best running time `\min_{c\in C}\E_\cD[\ell(c,z)]`
    • Construct algorithm that provably achieves it

Need conditions on `C` and `\cD` to make these possible

Tasks

Categories of `f` in this work:
  • Sorting
  • Delaunay triangulations
  • Convex hulls (upper hull)
  • Coordinate-wise maxima

Each input `z=(x_1,\ldots,x_n)`, where
`x_i` are all real values, or
`x_i` are all points in the plane

Conditions on outputs

  • Combinatorial objects
  • Includes certificates that allow verification in `O(n)` time
    e.g. for maxima:
    • sequence of maxima, and
    • for each dominated point, a witness point dominating it

Particular proof structure is a particular way
to model work that a correct algorithm must do

Conditions on algorithms

  • Not too much space or training samples
  • Correct for all possible inputs
    • Work done is `\Omega(n)`
  • Key operation on data is comparisons
  • Output determined by `\mathrm{compseq}(c,z)`, the sequence of comparisons
  • `\textrm{Work} = \Omega(n+|\mathrm{compseq}(c,z)|)`
  • Broad category of possible comparisons
    • Use "natural" comparisons in geometric setting


A comparison yields at most one bit of information

Entropy lower bounds

  • `f(z)` is a random variable, since `z` is
  • `f(z) = ` output of `c` using `\mathrm{compseq}(c,z)`
  • So `\E[|\mathrm{compseq}(c,z)|] \ge H(f(z))`, the entropy of the output
    • Shannon
  • Work lower bound is `\Omega(n + H(f(z)))`

Meeting the entropy lower bound (prior work)

A classical example fits these conditions:
entropy-optimal search trees

  • Given some sorted list `L` of values
  • Function `f(z)`:
    `\qquad` Real value `z\rightarrow` `j`-th interval containing `z`
  • `\Omega(1+H(f(z)))` comparisons
  • Achievable [M75] via entropy-optimal trees `T`





Conditions on `\cD`

  • We require `\cD = \prod_i \cD_i`
  • For `z=(x_1, x_2,\ldots,x_n)`, `x_i \sim \cD_i`
    • Each `x_i` independent of the others
    • Not all identical
    • Distributions `\cD_i` are:
      • Arbitrary
      • Unknown
      • Discrete and/or continuous
  • Algorithms here use polynomial space
  • There exist `\cD` (without independence) such that
    `\exp(\Omega(n))` space is needed for time `O(n + H(f_S(z)))`
    •

Results: meeting the entropy lower bounds

Under these conditions: comparison-based algorithms, proof-carrying output, product distributions...

  • Algorithms doing `O(n + H(f(z)))` comparisons and work
    • (plus `O(n\log\log n)` for convex hull)
    • `O(n^2)` training instances `z_k`
    • `O(n^2)` space
  • For given `\alpha \in (0,1]`,
    • `O(n + H(f(z)))/\alpha` comparisons
    • `O(n^{1+\alpha})` training instances `z_k`
    • `O(n^{1+\alpha} \log n)` space
  • Tradeoff is tight, even for sorting
    •

Sorting : The Typical Set `V`

  • Sorting algorithm uses a set `V` of "typical" values
  • `V` is built using training samples, as follows:
    • Let `W := \mathrm{sort}(z_1 \cup z_2 \cup ... \cup z_{\lambda})`
      • `\lambda := K \log n`, for a constant `K`
    • Let `V:=` the list of every `\lambda`-th value of `W`
      • `v_i = w_{\lambda i}`
      • `|V| = n`
  • `V` represents the overall distribution of `z`
    • We expect about one value from `z` in each interval `[v_j, v_{j+1})`

Sorting : Search Trees `T_i` on `V`

To use `V`, we build, for each `x_i`,
an entropy-optimal search tree `T_i` over `V`

As above:
  • Search random variable is bucket index `b_i:= j` when `x_i\in [v_j, v_{j+1})`
  • The search cost is `1+H(b_i)`
  • Additional training instances are used to build `T_i`

Sorting : The Algorithm

  • After training, the algorithm is:
    • For each `i=1..n`:
    `\qquad` locate `x_i` in the buckets using `T_i`
    For each bucket:
    `\qquad` sort the set of values falling in each bucket
  • Expected `O(1)` work/bucket, so total over buckets is `O(n)`
  • Searches are entropy-optimal
    •
  • So we're done, right?
    •

Analysis

  • We're not quite done
  • Although the `T_i` are individually optimal,
    it hasn't been shown that their cost is small
  • It remains to show that `\sum_i O(1+H(b_i)) = O(n+H(f_S(z)))`

Analysis via Coding

  • Independence `\implies \sum_i O(1+ H(b_i)) = O(n + H(b))`,
    `\qquad` where `b= (b_1,...,b_n)`
  • Note that `b` can be computed from `f_S(z)`,
    using `O(n)` additional comparisons:
    Sort the values `x_i` using `f_S(z)`
    Merge that sorted list with `V`, with `O(n)` comparisons
    Read off bucket assignments from merged list


So `b` can be encoded using
  • An encoding of `f_S(z)`, plus
  • `O(n)` bits for the comparisons


`H(b)\le` encoding cost ` = O(n+H(f_S(z)))`

Search work ` = O(n+H(b)) = O(n+H(f_S(z)))`

Delaunay Triangulations

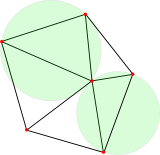
  • Given a set `z` of points,
    its Delaunay triangulation `f_T(z)` is a planar subdivision whose vertices are the points in `z`
  • If a triangle `T` has:
    • Vertices from `z`, and
    • No points of `z` in its circumscribed disk
  • Then `T` is a Delaunay triangle, with a Delaunay disk
  • A Delaunay triangulation comprises all such Delaunay triangles
    • (Ignoring the unbounded parts)

Sorting vs. Triangulation

  • Delaunay triangulation is like sorting, only more complicated
    • Actually, sorting can be reduced to Delaunay triangulation
  • We can view sorting as:
    `\qquad` find all open intervals `(x_i, x_{i'})` containing no `x_{i''}`, all from `z`
  • We can view finding the Delaunay triangulation as:
    `\qquad` find all Delaunay disks
  • Algorithm and analysis for triangulation generalizes that for sorting

Sorting::Delaunay as...

Sorting Delaunay Triangulation
Intervals `(x_i, x_{i'})` containing no values of `z` Delaunay disks
Typical set `V` Range space `\epsilon`-net `V` [MSW90, CV07],
Ranges are disks, `\epsilon = 1/n`
`\log n` training sample points per bucket `\log n` training sample points per disk
Expect `O(1)` values of  `z` in each bucket Expect `O(1)` points in each D. disk of `V`
Entropy-optimal search trees `T_i` Entropy-optimal planar point location `T_i` [AMMW07]
Sorted within each bucket yields
`f_S(V \cup z)` in `O(n)`		 Triangulated within each small region yields `f_T(V \cup z)` in `O(n)`
Removal of `V` from sorted `V \cup z` (trivial) Build `f_T(z)` from `f_T(V \cup z)` [ChDHMST02]
In analysis: merge of `f_S(V)` and `f_S(z)` to get `f_S(V\cup z)` In analysis: merge of `f_T(V)` and `f_T(z)` to get `f_T(V\cup z)` [Ch92]
In analysis: recover buckets `b_i` from sorted `f_S(V \cup z)` (trivial) In analysis: recover triangles `b_i` in `f_T(z)` from `f_T(V \cup z)`

Why the "easier" problems are hard

  • Delaunay triangulation includes convex hull
  • Hard to acount for work in proving points not on hull
  • Non-upper-hull `x_j, j=n/2+1,\ldots, n` easily proven by `\overline{x_1 x_{n/2}}`
    • Don't need to sort them
  • When points close to hull, have to sort
  • When `x_1,x_{n/2}` equally likely at two positions,
    none/some/all remain on upper hull




`x_1,\ldots,x_{n/2}` are fixed (singleton distributions)

`x_1,\ldots,x_{n/2}` are fixed (singleton distributions)

`x_1,\ldots,x_{n/2}` are fixed (singleton distributions)

Algorithms for maxima and hull

  • Both build set `V` (of horizontal coords of `x_i`s) and trees `T_i` for each `\cD_i` or related distributions
  • Strategy: search for each point `x_i` only as far down as is necessary for correctness
  • Maxima: sweep from right to left, maintaining leftmost maximum
    • Traverse `T_i` for each `x_i` that is
      not yet out, and might be rightmost not-swept
  • Hull: also build a polygonal curve so that any supporting line has little mass above it
    • Use that curve to help find certificates

Concluding Remarks

  • 😤 The results are pleasingly tight
  • 😥 😱 Not enough bang for buck: all that work for a `\log` factor
  • 😊 Novelty for me: the coding arguments
  • 😲 Are there stronger conditions that imply cheaper algorithms?
  • 😲 Are there broader conditions that allow interesting results?
    • `\qquad` Without full independence of each `x_i`, for example



Thank you for your attention