Improved Approximation Algorithms for Geometric Set Cover
Ken Clarkson |
Kasturi Varadarajan |
Bell Labs |
Univ. Iowa |
The set cover problem
- Given `bb(U)`, a set; here, a set of points
- Given collection `bb(S)` of subsets of `bb(U)`, here called "objects"
- Given `bb(M) subset bb(U)`, find the smallest subset `C` of `bb(S)` that covers `bb(M)`
For example: siting of basestations
- Objects are footprints of basestations, `bb(M)` is market area
- Footprint is area visible to basestation
- Choose from among discrete set of such footprints
- Often modeled as circular disks in the plane
- An idealization, esp. for directional antennas
Simplified cases of basestation siting
- Results here apply to a few simplifications:
- Fat triangles
- Visibility regions at points in a 1.5d terrain `approx` "guarding"
(A few) old set cover results
If `c := |bb(C)^{:**:} |`, `n := |bb(S)|`, can get within factor:
- `O(log n)`, with the greedy algorithm;
- `O(log c)`, for polytope approximation in `RR^m` [C94] ([L87][W88])
- `O(log c)`, when the VC dimension is bounded [BG]
- `O(1)`, polytope approximation in 3d [BG]
- Or `bb(M) subset RR^3`, `bb(S)` is a collection of halfspaces
- Or `bb(M) subset RR^2`, `bb(S)` is a collection of disks
- Use connection with `epsilon`-nets
New results: hypothesis
- If complement of `cup(R)` has roughly linear combinatorial complexity
- Random `R subset bb(S)`
- Decomposable into expected `f(r) = o(r log r)` simple regions,
`r:=|R|`

- For example, trapezoidization of complement of linear-complexity union
New results: conclusion
- Then approximation ratio is `f(c)//c = o(log c)`:
- Fat triangles `f(r) = O(r log log r)` [MPSSW], yields `O(log log c)` approx.
- Similar-sized fat objects with `t` boundary crossings `f(r) = lambda_(t+2)(r)` [Efrat]
- Regions bounded by Jordan arcs with `le 3` intersections `(alpha (n))` approx.[EGHPPSSS]
- In some cases `f(r)=O(r)` and ratio is `O(1)`:
- Similar-sized fat triangles [MPSSW], fat wedges [ERS]
- Arrangements of pseudo-disks [KLPS]
- 1.5d terrain guarding (matching [BMKM05]) *
- Unit cubes in `RR^3` [BSTY] *
Outline
- `epsilon`-nets
- An easy set cover problem
- Small `epsilon`-nets `=>` small covers
- Size of cover is within a constant factor of size of net
- As in [BG], [ERS]
- Small complement decompositions `=>` small `epsilon`-nets
- (Generalizing "shallow cuttings" [M])
- Particular case of [CF]
- 1.5d terrain guarding `=>` small complement decomposition
- Unit cubes: use fatness to create clusters, need only decompose boundary
`epsilon`-nets
- `epsilon>0` a given parameter
- Cover for easy-to-cover points `x in bb(M)_epsilon`
- `x in bb(M)_epsilon` if more than `epsilon {:| bb(S) |:}` objects contain x
- To construct: pick `r` objects from `bb(S)` at random
- Probability that:
- Given `x in bb(M)_epsilon` not covered is ` le (1-epsilon)^r`
- Some `x` not covered is `le |bb(M)_epsilon|(1-epsilon)^r`
- All `x` covered `ge 1 - |bb(M)_epsilon| e^(-r epsilon)`
- `r = O(log |bb(M)_epsilon|)//epsilon` is big enough
- [HW86]
`epsilon`-nets: equivalent points
- `log |bb(M)_epsilon|` could be large
- Maybe not in geometric settings
- Say that `x approx y` for `x,y in {: bbb()_epsilon :}` if `x in S iff y in S`, for all `S in bb(S)`
- Need only consider equivalence classes `bb(M)_epsilon/approx`
- For example, if VC dimension is `d'`, have `O(r^{d'})` classes for `R`
- Implies sample of size `O(d' \log (1//\epsilon))//epsilon` is a cover of `bb(M)_epsilon`
`epsilon`-nets: a different approach
- Sometimes `bb(U) setminus cup(R)` is "simple"
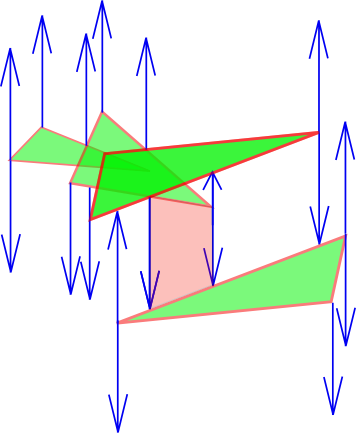
- For triangles, can make trapezoidal decomposition
- A trapezoid T is in decomposition iff:
- `d=O(1)` triangles "defining" `T` are in `R`
- None of the `|T|` triangles meeting `T` are in `R`
- `R` induces a collection of trapezoids `F_0(R)`,
`cup(F_0(R)) = bb(U) setminus cup(R)`
`epsilon`-nets using `F_0(R)`
- If `x in bb(M)_epsilon` and `x` in trapezoid `T`,

- Then `|T| ge epsilon |bb(S)|`
- (`|T|=` number of sets meeting `T`)
- There are `O(r^d)` such `T` possible, since `d` triangles define `T`
- For random subset of size `r`,
- Probability that some such `T` is not met by `R` is `O(r^d)(1-epsilon)^r`
- Similar to before, `r=(d \log(1//\epsilon))//epsilon` is big enough
- [C86]
Small `epsilon`-nets `=>` small covers
- Two approaches:
- Using "doubling" of objects [L87][W88][C92][BG94]
- Using LP relaxation [ERS], also observed by Kasturi
- Size bounds give `O(log c)` approximation
- Sometimes, can make `epsilon`-net smaller, even `O(1//epsilon)`
- Implies constant-factor approximations
Small `epsilon`-nets `=>` small covers: LP
- From [ERS]
- Tweak set system until every point is in `bb(M)_(1//2c)`
- Existence of solution of size `c` implies weights `w_S in [0..1]` with
`{:(sum_S w_S le c), (sum_{S ni x} w_S ge 1 text(for all) x in bb(M)):}`
- Make `bb(S)'`, a multiset, with `|~ w_S n//c ~|` copies of object `S`
- At least `n//c` sets contain each point, `2n` sets total
Small `epsilon`-nets `=>` small covers: doubling
- [L87][W88][C92][BG94]
- Tweak set system until all points in `bb(M)` covered:
- Find `(1//2c)`-net `E` of current `bb(S)'`; initially `bb(S)' := bb(S)`;
- For any `T in F_0(E)`, some `S in bb(C)` meets it;
- Double the multiplicity of all `S in bb(S')` that meet `T`;
- After `c` rounds:
- Factor increase of total multiplicity of `bb(S) le (1+1/{:2c:})^c approx sqrt{e}`;
- Increase of total mult. of `C ge 2`;
- Eventually `E` must be a cover
Small `F_0(R)` `=>` small `epsilon`-nets: alteration
- Use the alteration/mutation/repair method
- As in [CF], specialized to small `F_0(R)`
- Take random sample `R` of size `r:=1//epsilon`;
- Will find `epsilon`-net of size `O(f(r))`, `f(r)=E|F_0(R)|`
- Compute `F_0(R)`;
- "Patch up" regions in `F_0(R)`: find `epsilon_T`-nets for region `T`
- `epsilon`-net is union of `R` and `epsilon_T`-nets for each `T in F_0(R)`
Small `F_0(R)` `=>` small `epsilon`-nets: analysis
- How much patching up to do?
- Start from: with high prob., `R` is an `O((log r)//r)`-net;
- Need `epsilon_T` with `epsilon_T |T| = n//r`, or `epsilon_T= n//rj`, where `j={:|T|:}`
- To repair `T`, need `(jr//n) log (jr//n)` sample size, no more than `(jr//n)^2`
Small `F_0(R)` `=>` small `epsilon`-nets:
final analysis
- From [CS88],
`E sum_{T in F_0(R)} {:|T|:}^k = O(f(r)n^k//r^k)` - Or: expected proportion of `T` with `|T| ge i n//r` is `le e^{-i}`
- Take `k=2`, expected `sum_{T in F_0(R)} ({:|T|r:}//n)^2 = O(f(r))`
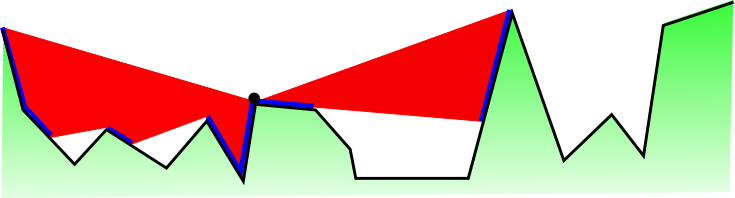
Terrain guarding: visibility
- Have terrain `P`, an `x`-monotone polygonal path
- Set `G` of point guards on `P`
- `g in G` sees a point `p` if:
- line segment `bar(gp)` does not meet region below terrain
More visibility
If also:- `x(g) lt x(p)`, then `g` sees `p` from the left
- `g` is the leftmost guard that sees `p` from the left, then `g` owns `p`
- No lower point at `x(p)` is seen by any guard, then `g` owns `x(p)` at `p`
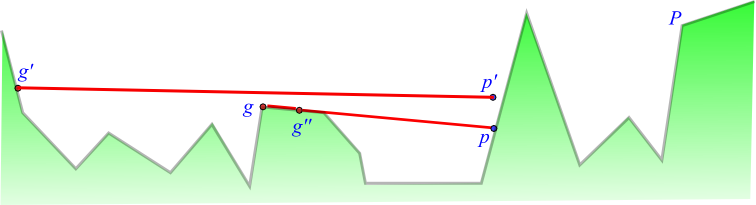
Why ownership?
- Any guarded point is also owned
- A set owns every point iff it sees every point
- Ownership is combinatorially simpler
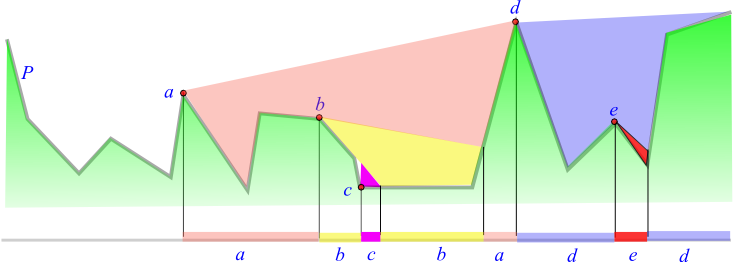
Order claim
- Generalizing [BMKM] slightly: for
- Guards `a`, `b`, points `p`, `p'`
- `x(a) lt x(b) le x(p) le x(p')`
- `a` owns `x(p)` at `p`, `b` sees `p'`
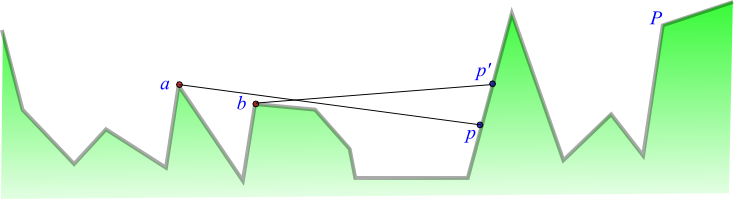
- Have:
- `a` also sees `p'`
- `b` must be below `bar(ap)`, `p` must be below `bar(bp')`
- So `b` cannot own `p'`
- No ownership pattern `a cdots b cdots a cdots b`
Davenport-Schinzel-orama
- Order claim implies ownership is `DS(m,2)` for `m` guards
- At most `2m-1` (left) ownership intervals
- Shows `|F_0(R)| lt 2r-1` for appropriate configuration system
- Implies small `epsilon`-nets for left visibility
- Combine with small `epsilon`-net for right visibility
- From small `epsilon`-nets, small covers
Concluding remarks
- Some other geometric set cover problems have `O(1)` approx.; any relation?
- Balls covering points in 3d?
- Thanks!