Sublinear-Time and Sublinear-Space Geometric Approximate Optimization for Some Problems Arising in Machine Learning and its Relatives

Ken Clarkson
IBM Almaden Research

joint with Elad Hazan and David Woodruff

Some Geometric Optimization Problems

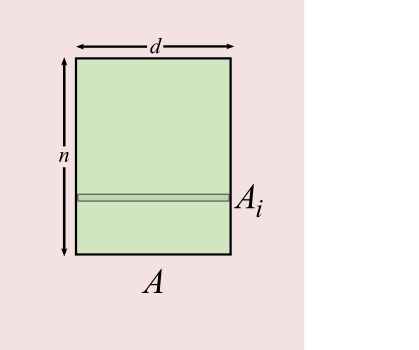
• Throughout, `n` points in `d` dimensions
• Or: `A` is an `n \times d` matrix
• Row `i` of `A` is `A_i`
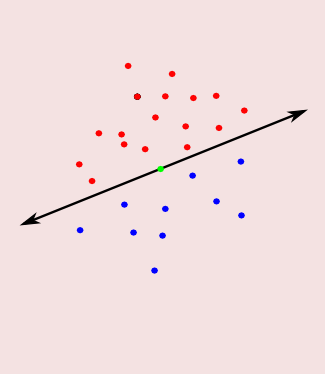
• Perceptrons: points are red or blue, split colors by a hyperplane
• A flavor of linear programming
• Minimum Enclosing Ball (MEB): find the smallest ball containing the points
• A flavor of quadratic programming

Our Results

• Sublinear-time approximation algorithms, and matching lower bounds
• Matching up to polylog factors
• Additive error `\epsilon > 0`
• Perceptron: `\tilde{\Theta}(\epsilon^{-2}(n+d))`, vs. classical `O(\epsilon^{-2}\nnz{A})`
• `\nnz{A}=` number of non-zero entries of `A`
• When `\nnz{A}=nd`, a big improvement
• MEB: `\tilde{\Theta}(\epsilon^{-2}n + \epsilon^{-1}d)`, vs. `O(\epsilon^{-1/2}\nnz{A})`
• Upper bound needs norms of points to be known
• Lower bound when center must be in convex hull of input
• Previous algorithm is in upcoming SODA
• Plus: $L_2$-SVM, $L_1$-SVM (to appear), kernelized (SVM), streaming, parallel, QP in simplex,...

MEB Formulation

• One formulation is $$\min_{x\in\reals^d} R_A(x) = \min_{x\in\reals^d} \max_{i\in [n]} || x - A_i^\top||^2$$
• Find the center `x` that minimizes the maximum squared distance
• `[n] \equiv \{1,2,\ldots, n\}`
• Equivalently, $$\min_{x\in\reals^d} \max_{\color{green}{p\in\Delta_n}} \color{green}{\sum_{i\in [n]} p_t(i)}|| x - A_i^\top||^2$$
• `\Delta_n \equiv` the unit simplex `\equiv \{p\in\reals^n | \sum_i p(i) = 1, p(i)\ge 0\}`
• Since maximizing `p` puts all its weight on the farthest point

Max `p` vs. Min `x`

• The "max player" tries to find the maximizing `p_t\in\Delta_n`
• For given `x`, a short-sighted response `p` has some `p(i)=1`
• Less short-sighted: `p_t(i) = p_{t-1}(i)\exp(\eta || x_{t-1} - A_i^\top||^2)`
• For suitable value `\eta`
• ...and also normalizing so that `\sum_i p_t(i) = 1`
• That is, a Multiplicative Weights (MW) update
• The "min player" tries to find the minimizing `x_t`
• For given `p`, the best `x` is `A^\top p`, the weighted centroid of the input points
• Less myopically, update `x_t` to `x_{t+1}` by a convex combination of `x_t` and `A^\top p_{t+1}`
• That is, an Online Gradient Descent (OGD) update

A Primal-Dual Algorithm

The Primal-Dual Algorithm is Not Too Bad

• Claim:  for `T=\tilde{O}(1/\epsilon^2)`, `\bar{x} = \sum_{\tau\in [T]} x_\tau/T` has $$R_A(\bar{x}) \le R_A(x^*) + \epsilon.$$
• Time per iteration is `O(\nnz{A})=O(nd)`
• Except for computing `A^\top p_t` and the squared distances `||x_t - A_i^\top||^2`, work is `O(n+d)`
• Since `||x_t - A_i^\top||^2 = ||x_t||^2 + ||A_i||^2 - 2A_i x_t`, need basically `Ax_t`
• We're assuming all `||A_i||` are known

Randomizing the Primal-Dual Algorithm

• We can use random estimates so that one iteration takes $O(n+d)$ total time
• To update $x_t$, pick $i_t$ with prob. $p_t(i)$, and use $A_{i_t}^\top$ instead of `A^\top p_t`
• `\E[A_{i_t}^\top] = A^\top p_t`, so update is the same in expectation
• To update `p_t(i)` to $p_{t+1}(i)$, estimate `||x_t - A_i^\top||^2` by:
• Pick $j_t$ with probability $x_t(j)^2$ (assuming `||x_t||=1`)
• Use $z_t \equiv A_i(j_t)/x_t(j_t)$ as estimate of $A_i x_t$
• $\E[z_t] = \sum_j [A_i(j)/x_t(j)] [x_t(j)^2] = \sum_j A_i(j) x_t(j) = A_i x_t$
• Estimate `||x_t - A_i^\top||^2 \approx v_t(i) \equiv ||x_t||^2 + ||A_i||^2 - 2z_t(i)`
• We call these estimation techniques $\ell_1$ and $\ell_2$ sampling, respectively

The Randomized Primal-Dual Algorithm is
Not Too Bad

• Claim:  for `T=\tilde{O}(1/\epsilon^2)`, the output vector `\bar{x} = \sum_{\tau\in [T]} x_\tau/T` has $$R_A(\bar{x}) \le R_A(x^*) + \epsilon.$$
• NB: same as for deterministic version
• Time per iteration is `O(n+d)`
• Can be much faster than deterministic version
• But maybe there's big multipliers hiding in the `\tilde{O}()`?

Randomized vs. Deterministic

• Noise added to distances to simulate `\ell_2` sampling
• Color: large `\color{red}{p_t(i)}`, small `\color{blue}{p_t(i)}`,
  HSL interpolation
• Black dot is center `x_t` for randomized
• Black dot with red ring is center `x_t` for det.
• After some iterations, similar behavior

Randomized vs. Deterministic for "real" data

• Ratio of farthest point distances, randomized/deterministic
• Very preliminary
• Some data sets from MLComp, with or without a single additional added outlier
• Here also, randomized `\approx` deterministic after 25 or so iterations
• To do: comparison with state of the art

Kernelization

• In kernel methods, the input `A_i` are lifted to points `\Phi(A_i)`
• `\Phi` is non-linear
• For some popular `\Phi()`:
• Dot products `\Phi(A_i)\Phi(A_j)^\top` can be computed from
• Dot products `A_iA_j^\top`
• We show:
• Good enough estimates of `\Phi(A_i)\Phi(A_j)^\top` can be computed from
• Good enough estimates of `A_iA_j^\top`
• E.g.: for the polynomial kernel `(x^\top y)^g`, use `g` independent estimates of `x^\top y`
• Increase in running time is additive `O(1/\epsilon^5)`

Remaining Questions

• How can the randomized algorithm possibly work?
• Analysis ingredients: regret bounds, concentration (tail estimates)
• Surely someone has done something very similar already?
• Related work, in particular using `\ell_1` sampling
• What does this have to do with low-rank matrix approximation?
• `\ell_2` sampling vs. sketching for matrix-product estimation

Ingredients of the Analysis:
Regret Bounds and Concentration

• Regret bounds for on-line convex optimization
• `x_t` does nearly as well, overall, as the best single `x`, for minimizing average distances to the `A_{i_\tau}`
• `p_t` does nearly as well, overall, as the best single `p`, for maximizing the averages of the distance estimates `v_t(i)`
• Concentration bounds for the estimators, such as:
  `\sum_{t\in [T]} v_t(i)` is close to its expectation `\sum_{t\in [T]} ||x_t - A_i||^2`
  for all `i\in [n]`

Concentration Bounds

• The `\ell_2`-sampling estimator has variance `\norm{A_i}^2\norm{x_t}^2`
• Assume that all such variances are `\le 1`, that is, all `\norm{A_i}\le 1`
• I've been lying: we don't quite use the estimator `v_t` as described
• We clip it to `\tilde{v}_t(i) \leftarrow \textrm{Clip}(v_t(i), 2/\epsilon)`, so that `|v_t|\le 2/\epsilon`
• Where `\textrm{Clip}(x,a) \equiv \min\{a, \max\{-a, x\}\}`
• We have `| \E[v_t(i)] - \E[\tilde{v}_t(i)] | \lt \epsilon`
• (Using here `\E[v_t(i)]\le 2`)

Concentrated Estimators via Variance Bounds

• `\sum_{t\in [T]} \tilde{v}_t(i) \approx \sum_{t\in [T]} \E[v_t(i)]` via a Martingale version of:
Theorem. Let `Y_1,\ldots,Y_T` be independent random variables with `|\E[Y_i]|\le 1` and `\Var[Y_i]\le 1` for all `i`. For `\epsilon, \delta>0`, there is `T\approx \log(1/\delta)/\epsilon^2` so that with probability at least `1-\delta`, $$| \sum_{t\in [T]} \textrm{Clip}(Y_t,2/\epsilon) - \sum_{t\in [T]} \E[Y_t]\, | \le T\epsilon.$$
• The proof follows from Bernstein's inequality and the claim about the expectation of the clipped version

Digression: Other Concentrated Estimators
from only Variance Bounds

• Another estimator with similar bounds:
• Split the `Y_i` into `\log(1/\delta)` groups of `1/\epsilon^2` each
• Take the median of the averages of each group
• Long known, e.g. in the streaming literature
• Both this median-of-averages and our average-of-clipped estimator are non-linear, which is surely inevitable
• It is also possible to get a concentrated estimator when the variance is bounded but unknown (Catoni)

Related Work: Coresets,
Low-Rank Approximation

• Coresets: small subsets of input points that specify approximation solutions
• Given `\epsilon`-coreset `C`, all input is inside `(1+\epsilon)\textrm{MEB}(C)`
• A variety of applications since introduced about a decade ago
• The rows `A_{i_t}, t\in [T]` comprise a coreset
• Together with columns `A_{:j_t}, t\in [T]`, specifies our solution
• For classifier results as well as MEB
• Akin to rows and columns of low-rank approximation
• Vaguely, kind-of, a bit

Related Work: Prior Primal-Dual Algorithms

• Our perceptron algorithm finds $$\min_{p\in\Delta_n} \max_{x\in\Ball_d} p^\top Ax$$
• Previous work [GK,KY] found sublinear approx. algorithms for $$\quad\quad\min_{p\in\Delta_n}\max_{x\in\color{green}{\Delta_d}} p^\top A x$$
• Optimal mixed strategies for a game
• Assumes bound for `||A_i||_\infty`
• Better results: small relative error
• Easier(?) problem, because `\ell_1` sampling is easier than `\ell_2` sampling
• `||A_i||_\infty \le ||A_i||_2`, or `\Delta_d\subset\Ball_d`
• (The solution to `\max_{p\in\Ball_n}\max_{x\in\Ball_d} p^\top A x` is `||A||`)

`\ell_2` Sampling vs. Sketches

• Another possible approach: sketching/JL/random projections
• Map each `A_i` to `\tilde{A}_i\in\reals^m` with `m=O(\epsilon^{-2}\log(n/\delta))`
• This can be done so that `A_i A_j^\top \approx \tilde{A}_i \tilde{A}_j^\top` for all `i,j\in [n]`
• Solve the problem in "sketch space", and then map back
• Sketching works here, but is slower and takes more space
• Are there other applications where `\ell_2` sampling can be used instead of sketching?
• "Feature selection" for classifiers
• Matrix product
• Probably: nearest-neighbor search

`\ell_2` Sampling as Low-Rent Feature Selection

• Here we showed that `\ell_2` sampling estimates `Ax` in `O(n+d)` time
• With variance `\norm{A_i}^2\norm{x}^2` for estimate of `A_ix`
• By clipping and averaging, this gives a concentrated estimator
• Only an upper bound on the row norms of `A` is needed
• This could be applied to linear classification
• Weight vector is `x`
• Rows of `A` comprise the vectors to classify
• Sample `x` beforehand, storage `O(\epsilon^{-2}\log(q/\delta))`
• `q` bounds the number of rows of `A`
• Storage of `x` as for sketching, but classification is faster

Matrix Product via `\ell_2` Sampling

• We can extend from vector `x` to matrix `B`
• Pick row `i` of `B` with probability `Q_i\equiv \norm{B_i}^2/\norm{B}_F^2`
• Return outer product `A_{:i}B_i/Q_i` as estimate of `AB`
• Variance is about `\norm{A}_F^2\norm{B}_F^2`
• Can be repeated for concentrated estimator
• Needs upper bound on row norms of $A$
• Very similar to classical sampling of [DKM]
• (Also very similar to some sampling schemes for regresion)
• But: nearly oblivious to `A`

Concluding Remarks

• Bounds are tight for basic perceptron and MEB algorithms
• Kernel methods need improvement in additive `O(\epsilon^{-5})` term
• Stochastic gradient algorithms are of course also related
• Where else can `\ell_2` sampling supersede sketching?
• Are there `\tilde{O}(\nnz{A})` algorithms for these problems?