Metric Spaces, Nets, Measures, Dimensions, and Search

Ken Clarkson
IBM Almaden Research

Nearest Neighbor Search: the Problem

• Given
  • A set of sites (points) `S \subset U`
  • Distance function `D(x,y)` for `x,y\in U`
• Build a data structure so that:
Given `q \in U`, the closest site $$\argmin_{x\in S} D(q,x)$$ can be found quickly

Nearest Neighbor Search: Synonyms

• Considered for at almost forty years, called:
• Post Office problem (McNutt, '72)
• Best match file searching [BK73]
• Index for similarity search [HS03]
• Vector quantization encoder
• Fast nearest-neighbor classifier

The Distance Function as a Metric "Black Box"

• I will shallowly survey various data structures, concepts, conditions, related to NN
• Will assume distance is a metric, and otherwise a black box
• Input to algorithms is only some user-defined function
  float Dist(int, int)
• Pluses for this level of generality:
  • Simplicity
    • With only that black box, how complicated could an algorithm get?
    • Although some constructions are amazingly complicated
  • Ideally, something to try first, like qsort, "OK most of the time"
  • Clarity: what conditions are really needed for a good data structure?
• Minuses:
  • Many distances/similarities of interest are not metrics
  • For any given distance function, special case approaches will be faster

Goals for NN Search Data Structures

• The algorithms I'll describe are "structure-oblivious"
  • They are fast for points on a line, without being told the input comes from points on a line
• But for some input, brute force is the best
  • A subgoal: graceful degradation to brute force, especially for space
  • Hippocratically: first, do no harm
• Mostly I'll talk about exact algorithms
  • The NN, not the third closest, not within `1+\epsilon`...
  • This is best for most applications
  • In high dimension, every site is an approximate NN
  • Correct, and heuristically fast,
      not
    Fast, and heuristically correct
    • However: via filtering, approximate queries can help answer exact queries
    • For some constructions, analysis involves approximation

Metric Spaces: Definition and Repairs

• Isolation: `x \ne y` implies `D(x,y) > 0`
  • If not: pseudometric, fix with equivalence classes
• Symmetry: `D(x,y)=D(y,x)`
  • If not: quasimetric; `\hat D (x,y) \equiv (D(x,y) + D(y,x))/2`
• Triangle Inequality: `D(x,z) \le D(x,y) + D(y,z)`
  • If not: semimetric; metric completion is
    `\hat D (x,y) \equiv \inf_k \sum_{i\in [k]} D(z_i, z_{i+1})`, `x=z_0`, `y=z_{k+1}`
  • Or: snowflake (discussed later)

New Metrics from Old

• `L_p`: `\hat U\equiv U_1 \times U_2 \times \cdots \times U_m`, `\hat D(x,y) \equiv [\sum_i D_i(x_i,y_i)^p]^{1/p}`
• Strings over `U`:
  • For `x=uaw` and `y=ubw`, `\hat D(x,y) \equiv D(a,b)`
  • (including distance to null character)
  • Take metric completion
• Nonnegative combinations: `U_1=U_2= \cdots =U_m`,
  For given `\alpha_1 \ldots \alpha_m`,
  `\hat D(x,y) \equiv \sum_i \alpha_i D_i(x,y)`

New Metrics from Old: Subsets

• Distances on subsets `A,B \subset U`
• Hausdorff: `\hat D(A,B) \equiv \max\{\sup_{a\in A} D(a,B), \sup_{b\in B} D(b,A)\}`
  • `D(a,B)\equiv \inf_{b\in B} D(a,b)`
  • That is: smallest `v` so that every point of `A` has some `b\in B` within `v`, and vice versa
  • Have isolation if sets are compact
• Given measure `\mu` on `U`, distance `\hat D(A,B)\equiv \mu(A \Delta B)`
• Any analog for kernel distance for general spaces?

New Metrics from Old: Numeric Transforms

` \left. \eqalign{ &f : \reals\rightarrow\reals \\ &f(0) = 0 \\ &f \textrm{ nondecreasing } \\ &f \textrm{ concave}\\ }\right\} \Rightarrow ` `\hat D(x,y) \equiv f(D(x,y))` also a metric
• `f(z) = z^\epsilon` for `\epsilon \in [0,1]`, the "snowflake"
  • Alternate fix for semimetric: extreme case is `\epsilon` close to 0, `\hat D(x,y)\approx 1`
• `f(z) = z/(1+z)` : distances are in `[0,1]`
• `f(z) = \min\{z, 1\}`

Numeric Transforms, II

• `f(z) = \log(1+z)`
  • For values `a` and `b`, `D(a,b) \equiv \log_2( 1 + |a-b|)` is a metric
  • The number of bits to delta-encode integer `b`, given `a`
• `f(z) = 1-\exp(- \lambda z), \lambda > 0`
• `\hat f (z) = \sqrt{f(z^2)}`, for `f(z)` satisfying the conditions
• `f(z) = \sqrt{1-\exp(- z^2)}`
  • `f(\norm{x-y})` is the distance based on the Gauss kernel, as used in ML
  • A Schoenberg transform: if `D(.,.)` is Euclidean, so is `\hat D(.,.)`
  • Schoenberg characterized all such transforms

Numeric Transforms, III

• `f(z) = \left\{ \eqalign{ & 1 - (1-z)^n & z\in [0,1] \\ &1 & z\ge 1}\right.`
• `\approx 1 - \exp(- n z)`
• If `g` and `h` are functions of a random variable `x`, then
  `D(g,h) \equiv \Prob\{g(x) \ne h(x)\}` is a metric
• If `x_1, x_2,\ldots` are `n` independent instances of `x`, then
  `\hat D(g,h) \equiv \Prob\{\exists x_i, g(x_i) \ne h(x_i)\} = f(D(g,h))`

The Biotope Transform

• Given `a \in U`, the biotope or Steinhaus transform is $$\hat D(x,y) \equiv \frac{2D(x,y)}{D(x,a) + D(y,a) + D(x,y)}$$
• For finite sets `A`, `B`, distance `D(A,B)=|A \Delta B|` and `a=\{\}`, get
  $$\eqalign{ \hat D(A,B) & = & \frac{|A \Delta B|}{|A| + |B| + |A \Delta B|}\\ & = & \frac{|A \Delta B|}{|A \cup B|} } $$

Biotope Distance : a.k.a.

• Marczewski-Steinhaus [MS58] in ecology, 1040 hits
• Tanimoto [RT60] in chem and genetics, 113000 hits
• Jaccard [J01] in CS and genetics, 146000 hits
• Set similarity in TCS [Cha02]
• Resemblance in TCS/Web [B97]

Subset Biotope

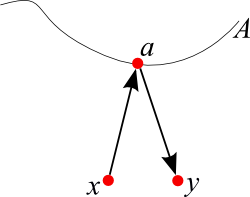
A Metric Space Scaled to Local Feature Size

• Recall that `F: U\rightarrow \reals` is Lipschitz when `|F(x)-F(y)|\le D(x,y)`
  • For `y\in U`, `F_y(x)\equiv D(y,x)` is 1-Lipschitz
• For Lipschitz functions `F`, biotope transform implies $$ D_F(x,y) \equiv \min \{ 1, \frac{2D(x,y)}{D(x,y) + F(x) + F(y)} \} $$ is a metric.
• `D_F(x,y) \approx D(x,y)/F(x)` when `D_F` is small

So What?

• These repairs and transforms are mostly well-known
• It's just nice that: they apply to any metric

NN Search: Using the Triangle Inequality

• When answering a query for `q`, what can be learned?
• Only `D(q, p)` for various `p\in S`
  • When `D(.,.)` is only given as a black box
  • Ignoring the possibility of using `D(q,p)` for `p\notin S`

Using the Triangle Inequality

• Brute force: try all `p\in S`, take the minimum
  • Often the best approach
• Otherwise: use metric properties to infer bounds on unknown distances
• At a particular moment, data structure has evaluted `D(q, p)`, for `p\in P\subset S`
• What do these distances imply about `D(q,s)` for `s\in S\setminus P`?
• Of course, `D(q, S) \equiv \min_{p\in S} D(q,S) \ge D(q, P)`

Using Distances to `P\subset S`

• For a given point `p\in P`, query point `q`, point `s\in S\setminus P`,
• apply the triangle inequality in all three ways to `\{q,p,s\}`:
  `\eqalign{ D(q,s) & \le D(q,p) + D(p,s) \\ D(q,p) & \le D(q,s) + D(s,p) \\ D(s,p) & \le D(q,p) + D(p,s) \\ }`
• Re-arrange:
  `\eqalign{ D(q,s) & \ge D(q,p) - D(p,s)\\ D(q,s) & \le D(q,p) + D(s,p) \\ D(q,s) & \ge D(p,s) - D(q,p) \\ }`
• More compactly:
  ` D(q,p) + D(s,p) \ge D(q,s) \ge | D(q,p) - D(s,p) |`
• So $$\min_{p\in P} (D(q,p) + D(s,p)) \ge D(q,s) \ge \max_{p\in P} | D(q,p) - D(s,p) | \equiv D_P(q,s)$$
• If `s` has `D_P(q,s) > D(q,P)` then $$D(q,s) \ge D_P(q,s) > D(q,P) \ge D(q,S),$$ so `s` is not NN to `q`
  • (For `P=S=U`, `D_P = D`, a Kuratowski embedding into `\ell_\infty`)

AESA

• The AESA algorithm maintains `P\subset S` with `D(q,p)` known for `p\in P`
• Distances among all `p,p'\in S` are pre-computed
• Algorithm sketch:
  Pick `c\in S` arbitrarily; // `P\gets \{c\}`
  repeat forever:
    Pick `c` with smallest `D_P(q,c)`
    Compute `D(q,c)`, `P\gets P\cup\{x\}`
    for live `s`: update `D_P(q,s)`; if `D_P(q,s) > D(q,P)` then kill `s`;

Orchard Algorithm

• Another approach, using NN of `q` in `P`
• `p \overunder{v}{P}{\longleftarrow} q \overunder{}{S}{\longrightarrow} a `
• `p \overunder{v}{P}{\longleftarrow} q \overunder{\le v}{S}{\longrightarrow} a `
• ...and so: if `D(s,p) > 2D(q,p)`, then `s` is not NN to `q` in `S`
• This suggests: for each `p\in S`, list `L_p` of sites, sorted by increasing `D(p,s)`
  Pick `c\in S` arbitrarily; // `P\gets \{c\}`
  repeat forever:
    for `s\in L_c`:
      if `D(c, s) > 2D(c,q)`: return `c`;
      if `D(q,s) < D(q,c)`: `c\leftarrow s`; break; // `P\gets P\cup\{s\}`

Using Less Space

• `\Theta(|S|^2)` space is too much
• Alternatively: for some `N\subset S`, precompute only `\{D(p,s)\}_{p\in N, s\in S}`
  • Adjust algorithms accordingly
  • For Orchard, lists `L_p` for only `p\in N`, change list only to site in `N`
  • For AESA, don't update `D_P` when for `s\notin N`
• What is a good `N\subset S`?
  • Suppose `\epsilon \leftarrow \max_{s\in S} D(s,N) = D(S,N)` is small
  • That is, `N` is a minimal `\epsilon`-cover
  • Then for any `q\in U`, `|D(q,s) - D(q,p)| \le D(s,p)\le \epsilon` for `p\overunder{}{N}{\longrightarrow} q`

`\epsilon`-nets and the Greedy Algorithm

• `N(\epsilon) = N \subset U` is an `\epsilon`-net if it is both an:
• `\epsilon`-packing: all `p\in N` are at least `\epsilon` from `N`
  • `D(p, N\setminus\{p\})\ge \epsilon` for `p\in N`
• `\epsilon`-covering: all `p\in U` are at most `\epsilon` from `N`
  • `D(p,N) \le \epsilon` for `p\in U`, so `D(N,S)\le\epsilon`
• Not range-space `\epsilon`-nets
• A greedy algorithm for nets [G85]:
  `N \leftarrow \{\}`
  repeat until done:
    `N \leftarrow N\cup \{ \argmax_{q\in U} D(q,N) \}`;
  

Greedy Construction Properties

• Optimal approximation algorithm, in a sense [G85][ST85]
• Used in building NN data structures [Bri95][WOj03][C03][HPM05]
• Bawden-Lajiness algorithm in comp. chem.
• Farthest Point Sampling in image proc. [ELPZ97]
• Not far from Chew's algorithm for building triangulations

Approximate Nearest Neighbor Searching

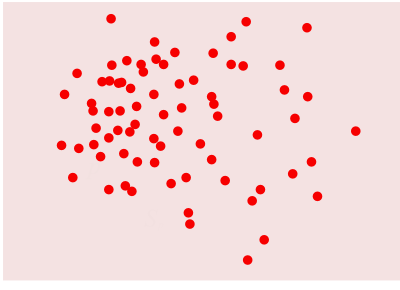
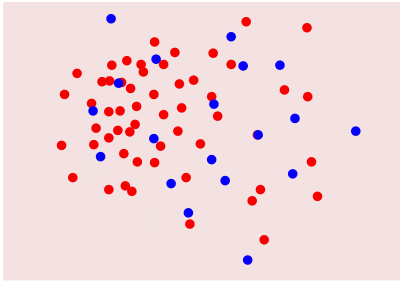
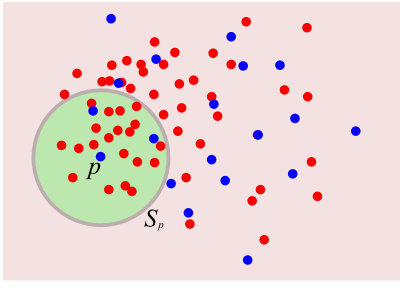
• Divide-and-conquer approach for approximation
• Space `(U,D)`, sites `S \subset U`,
  `\diam\, S\equiv \max_{p,p'\in S} D(p,p') = 1`
• Pick `\delta \le 1`, find `\delta^2`-net `N \subset S`
• Recursively build data structure,
  for each `S_p \equiv B(p, 3\delta) \cap S`, `p \in N`
• For given `q`: find nearest `p \in N`; recursively search `S_p`

Approximate NN Searching, Correctness

• This gives a `1+\delta` approximation algorithm
• From
  `p \overunder{\qquad\quad}{N}{\longleftarrow} q \overunder{v}{S}{\longrightarrow} a \overunder{\le\delta^2}{N}{\longrightarrow} p_a`
• We have
  `p \overunder{\le v + \delta^2}{N}{\longleftarrow} q \overunder{v}{S}{\longrightarrow} a \overunder{\le\delta^2}{N}{\longrightarrow} p_a`
• If:
  • `\delta \le v`,
    then `D(p,q) \le D(q,S) + \delta^2 \le D(q,S)(1+\delta)`
    • `p` itself is within a `1+\delta` factor of the NN distance to `q`
  • `\delta\ge v`,
    then `D(a,p) \le 2v + \delta^2 \le 2\delta+\delta^2\le 3\delta`
    • So `a\in S_p`, and searching `S_p` will yield `a`

Approximate NN Searching, Analysis

• (Deferred, while I tell you some fun facts about `\epsilon`-nets etc.)

Nets as Roadmaps: Motion Planning

• Consider moving a small object (a point) among obstacles
• Want a plan to move from `a` to `b`
• By using more dimensions, can model more complicated motions and objects

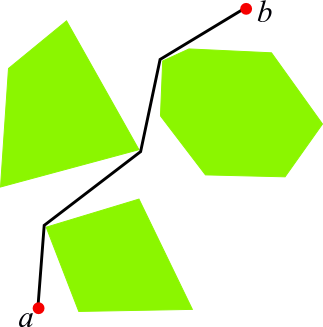
Nets as (Non)-Probabilistic Roadmaps

• Original Approach:

• Pick points in "free" space at random
• Find straight-line paths between nearby points
• Random points are nice, but
• `\epsilon`-nets (low dispersion) are nicer
• Grid points seem to work ok, Sobol sets, etc.

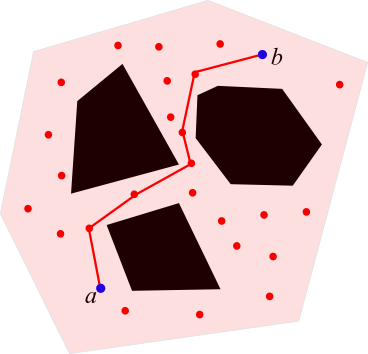
Nets as Roadmaps, Analysis

• Consider case where shortest path from `a` to `b` is a curve
• Suppose `N` is a `\delta^2`-net, `\delta\le 1`, `\diam U = 1`
• Suppose every `x,y \in N \cup \{a,b\}` with `D(x,y)\le 2\delta` are connected
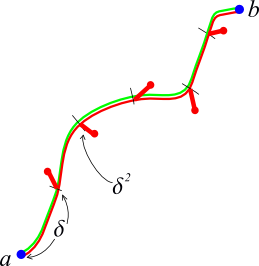
• Then this scheme has `2 \delta ` overhead:
• Split path into segments of length `\delta`
• Detour to `N` at each split, adds `\le \frac{1}{\delta} (2\delta^2) = 2\delta`
• Using triangle inequality, path along `N` is not longer

Nets as "Beacons" or "Landmarks"

• In networks: pick a net `N`
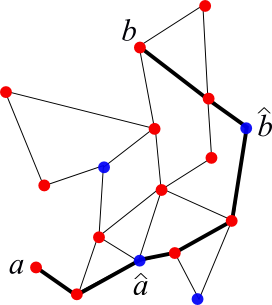
• To route from `a\rightarrow b`:
• Let `\hat a` be nearest to `a` in `N`
• Let `\hat b` nearest to `b` in `N`
• Walk `a \rightarrow \hat a \rightarrow \hat b \rightarrow b`
• Simpler addressing, simpler network
• Collection of distances to landmarks also used as a "coordinate system"

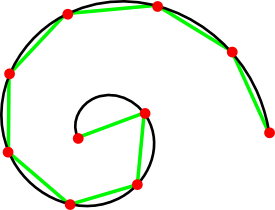
Nets as Vertices in Approximations

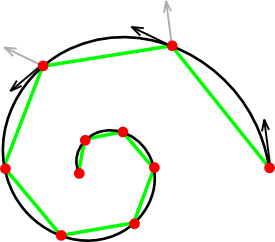
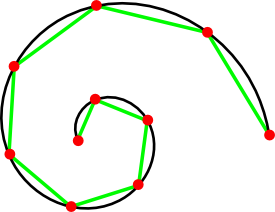
• Polygonal approximation of smooth curves:
• Pick a distance measure for points on curve
• Pick an `\epsilon`-net using that distance
• Connect the dots
• Due to McClure/Vitale, 1975; for `d>1`, by Gruber, Schneider,...
• More generally: vertices of meshes that approximate smooth surfaces [HG99] [C06]
  • Under a metric based on geodesic distance and curvature
  • `\approx` Dudley's approximation of convex bodies

What Distance Measure?

• Could use:
  • Arc length, but misses large curvature
  • Turning angle, but misses scale
  • Sum of both, works ok, or distance weighted by `\sqrt{\kappa(x)}`
    • `\kappa(x)` is the curvature

Arc Length

Turning Angle

Both

Nets as Vertices of Graded Triangulations

• Given a region and "walls", split into triangles so that:
• Triangles are close to equilateral
• Triangle edges don't cross the walls
• Triangles must be small near small features, get bigger gradually
• Implies a Lipschitz "local feature size"
  `F(x)` at point `x`
• An `\epsilon`-net in the metric scaled by `F` gives the vertices of a good graded triangulation

Building a triangulation

`\epsilon`-Nets: Also....

• `\epsilon`-sparse `\epsilon`-samples, for surface reconstruction [AB98]
  • Under a metric scaled by a local feature size, based on distance to the medial axis
  • Conditions under which a surface (in `\reals^k`) can be reconstructed from a point cloud sample
• Landmarks for witness complexes [dSC04]
  • `\approx` a local feature size inferred from the data

Non-Greedy Construction

• Greed is good, but not always best
• [HS85] For `p \in U`, in arbitrary order:
• If `D(p, N) > \epsilon`, add `p` to `N`
• Avoids global accurate computation of distances
• Since the choice of `p` is arbitrary, can pick `p` based on additional conditions
• For example: pick uncovered `p` so that `B(p, \epsilon)` contains the most points of `U`

Differently Greedy: `\epsilon`-cover with Outliers

• Suppose there is a `k`-point `\epsilon`-cover `O` for `m \le |U|` points
• Then the following constructs a `k`-point `3\epsilon`-cover for at least `m` points [CKMN01]
  `N \leftarrow \{\}`, `U' \leftarrow U`
  repeat `k` times:
    Find `p\in U` with max `|B(p,\epsilon)\cap U'|`
    `N \leftarrow N\cup \{p\}`;
    `U'\leftarrow U'\setminus B(p, 3\epsilon)`;

Cover with Outliers, Hints

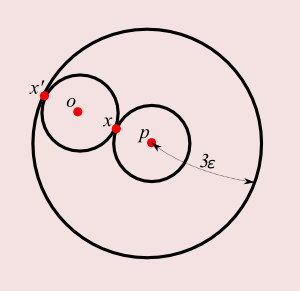
• For `p\in N` and `o\in O`:
  From `p\frac{\quad \le\epsilon\quad}{} x \frac{\quad \le\epsilon\quad}{} o \frac{\quad \le\epsilon\quad}{} x'`
  if `B(p,\epsilon)\cap B(o,\epsilon)\ne \{\}`,
  then `B(p,3\epsilon) \supset B(o,\epsilon)`
• So for first point `p_1\in N`, there is `o_1\in O` with
  `B(p_1,3\epsilon) \supset B(o_1,\epsilon)`
• It turns out that `N` and `O` can be ordered so that, for `k'\in [k]`
  `\cup_{i\in[k']} B(p_i,3\epsilon) \supset \cup_{i\in[k']} B(o_i, \epsilon)`

Non-`\epsilon`-Nets: Cover-like

• Random subsets
• Some quality measures are analogous to cover's
  `\max_{p\in U} D(p,N)`
• `k`-medians, minimizing `\sum_{p \in U} D(p,N)`
• `k`-means, minimizing `\sum_{p \in U} D(p,N)^2`

Approximation to `k`-means sets

• Another well-distributed set:
`N \leftarrow \{p\}`, `p\in U` arbitrary
repeat `k` times:
  Pick `p\notin N` with probability `\propto D(p,N)^2`
  `N \leftarrow N\cup \{p\}`;

• `O(1)` approximation for some data [ORSS]
• `O(\log k)` approximation in expectation [AV]
  (`k`-means`++`)
• For "smooth" `U`, `\epsilon`-nets are good for `k`-means as well

Non-`\epsilon`-Nets: Packing-like

• Minimize energy `\sum_{p,p' \in N, p\ne p'} D(p,p')^{-v}`
  for some `v>0`
• Natural model for repelling particles, distribution of competing plants
• Smoothness allows differentiation w.r.t. `p`
• Aids proof of [M75]:

  Random projection almost always preserves Hausdorff dimension

  • For a dimension `d` set, to a dimension `d' \ge d` set

Other Energies

• Instead of a sum of `D(p,p')^{-s}`, other functions of `D(p,p')` have been proposed
• Most generally: minimize an energy `\sum_{p,p' \in N, p \ne p'} g(D(p,p'))`,
  for some `g : \reals \rightarrow \reals`
• For example, the frame potential `g(x) = -x^2(1-x^2/4)` [BF01]
  • For points on a Euclidean sphere, equivalent to `\sum_{p,p'\in N} [p^\top p']^2`

Density Nets

• `D_k(p, U) \equiv` distance to `k`-NN of `p` in (finite) `U`
• Density net `N`: for all `p \in U`,
  `D(p, N)\le 2 D_k(p, U)`
• Follows density of `U`, like a random subset, but more evenly distributed
• Density nets of size `|U|/k` exist [CDG06][LZ08]
• For `p \in U`, in increasing order of `D_k(p,U)`:
  • If `D(p, N) > 2D_k(p,U)`, add `p` to `N`

Dimension and Approximate Measure

• The `\epsilon`-net size `|N(\epsilon)|` as `\epsilon \rightarrow 0` appears in many analyses
• The box dimension `d_B` is the `d` so that `|N(\epsilon)| = 1/\epsilon^{d+o(1)}` as `\epsilon \rightarrow 0`
  • Or equivalently, `d_B = \log{|N(\epsilon)|} / \log(1/\epsilon) + o(1)`
  • If `d_B` is not an integer, the set is a fractal
  • There are sets for which the `1/\epsilon^{o(1)}` is not a constant factor
• Equivalently, `d_B` is a critical value of the `t`-content `|N(\epsilon)|\epsilon^t`
  • Critical because `t`-content is infinite for `t < d_B`, zero for `t > d_B`
  • For a `d`-manifold, the `d`-content is `\approx` its surface area
  • If a `t`-content exists, there is a dimension for it

Box Dimension Equivalents

• Could use covering number ` C (\epsilon)` instead of `|N(\epsilon)|`
  • Constant factor doesn't matter in the asymptotic expression
• `d_C` is critical value of `t`-content

  `\lim_ {\epsilon \rightarrow 0 } C (\epsilon) \epsilon^t = \lim_ {\epsilon \rightarrow 0 } { \epsilon^{t - d_C + o(1)} }`

  • "Critical" because limit is zero for `t>d_C`, infinite for `t

Hausdorff Dimension

• Many other `t`-contents give a dimension
  • ...characterizing the limiting behavior of the content
• `\epsilon`-cover ` E` of balls has:
  • `\diam(B)\le \epsilon` for `B\in E`
  • `U\subset \cup_{B\in E} B`
• The critical value of the `t`-content

  `\inf_{ E \text{ an } \epsilon \text{-cover} } \sum_{B \in E} {\diam (B)^t} `

• ...is the Hausdorff dimension
• More balls than ` C(Z,\epsilon)`, but small ones count less

Box Dimension: Problems with Finiteness

• Asymptotic definition is problematic for point clouds and other finite spaces
  • If `U` is finite, `d_B=0`
• If `U` is a `d`-manifold, its measure (surface area) `\mu(U)` has
  `|N(\epsilon)|(\epsilon/2)^d \le \mu(U) \le |N(\epsilon)| \epsilon^d`
• So `d\approx \frac{\log |N(\epsilon)| - \log\mu(U)}{\log(1/\epsilon)}
• text

Box Dimension: Problems with Finiteness

• For finite `|U|`, `d_B=0`, but even for infinite `U`, `|N(\epsilon)|` may take awhile to be in asymptopia
• From a distance, set seems to be a line
• ...so initially, `|N(\epsilon)|` grows as `1/\epsilon`
• Closer inspection...
• ...reveals a more two-dimensional structure
• But even closer, back to 1d

• Consider also: a ball of yarn (Mandelbrot)
• Estimation of `d` from a point cloud depends on the scale of measurement `\epsilon`

Coping with Finiteness: Extremal Graphs

• For `n` sites `S`, let `\delta_{1:n}` denote the average NN distance
  `\frac{1}{n}\sum_{p\in S} D(p, S\setminus\{p\})`
• When a point cloud `S` is uniformly distributed on its `d`-manifold,
  `\delta_{1:n} = \Theta(n^{-1/d})`
  • Where `\Theta` constant depends on surface area `\mu`
• So `d \approx -\frac{\log n}{ \log \delta_{1:n}}`
• Similarly for other extremal graphs, like TSP, MST, matching,... [BHH59][CH04]
• Accuracy still a problem, but the scale of measurement is "chosen by the data"

Energy Dimension

• The energy `I_v(N) \equiv \frac{1}{n^2}\sum_{p,p' \in N, p\ne p'} D(p,p')^{-v}`
• For a `d`-manifold [HS04], $$\inf_{N\subset U, |N|=n} I_v(N) = n^{v/d - 1 + o(1)}$$
• Can define energy dimension for a general space as such a `d`

Even More Dimensions: Metric Measure Spaces

• To a general metric space `(U,D)`, we add one more structure: a measure `\mu`
  • Generally assume `\mu(U)=1`, that is, a probability distribution
• We can consider sets of sites `S` that are independently `\mu`-distributed
• Sometimes use empirical estimator `\mu(A) \approx |A \cap S|/n`
• Now `\E_S[\delta_{1:n}]` is defined, and gives a dimension estimator

Quantization Dimension

• Consider the `k`-means objective function value, as applied to all of `U`: $$V_n \equiv \inf_{N\subset U, |N|=n} \int D(x,N)^2 dx$$
• The quantization dimension is the `d` so that
  `V_n = n^{-2/d + o(1)}` as `n\rightarrow\infty`
• Empirically, perhaps `\sum_{p\in S} D(p,N)^2/|S|`
• Can substitute `v > 0` for `2`

Pointwise Dimension

• At `p \in U`, the pointwise dimension `\alpha _\mu (p)` is the `d` so that
  `\mu(B(p,\epsilon)) = \epsilon ^{d+o(1)}` as `\epsilon \rightarrow 0`
• Or, `\alpha _\mu (p) = \lim_{\epsilon \rightarrow 0} \frac{\log\, \mu(B(p,\epsilon))}{\log \epsilon } `
• Letting `\delta_{1:n}(p)\equiv D(p,S)` for random `S` we have [CD89]
  `\alpha_\mu(p) = \lim_{n \rightarrow \infty} {\log(1/n)}/{\log \delta_{1:n}(p) }`
• Heuristically:
• choose `\epsilon_n` such that `\mu(B(p,\epsilon_n)) = 1/n`
• have `\delta_{1:n}(p) \approx \epsilon_n`
• `{1/n} = \mu(B(p,\epsilon_n)) \approx \epsilon_n^{\alpha_\mu(p)} \approx \delta_{1:n}(p)^{\alpha_\mu(p)}`

Pointwise Dimension and Others

• Tao et al.: use estimates of pointwise dim. to predict NN search costs for nearby points
• Used in graphs for routing [GZ04]
• a.k.a. local dimension, Hoelder exponent
• Multi-fractal analysis uses function `f_\mu(\alpha)`
  • `\equiv` Hausdorff dimension of set of points of pointwise dimension `\alpha`
• Also related to energy and information dimensions

Doubling Dimension

• The doubling dimension is the `d_A` such that every ball of radius `r` can be covered by `2^{d_A}` balls of radius `r/2` [L67] [A83]
• If `d_A` is bounded:
  • Any `\epsilon`-cover of size `v` implies an `\epsilon/2^k`-cover of size `2^{kd_A} v`
  • ...so `\epsilon`-nets have size `O(1/\epsilon^{d_A})`
• `d_A` is bounded iff a "sphere-packing condition" holds:
  at most `4^{d_A}` points in `B(p,r)` can be farther than `r/2` from all other points in `B(p,r)`

Doubling Dimension, More About

• For manifolds:
  • Have bounded doubling dimension `d_A` (locally) if reach (distance to medial axis) of manifold is positive [DF08]
• If a point cloud has `d_A` bounded, can embed (preserving distances approximately) in `\reals^{O(d_A)}` [IN07]
• Subsets inherit bounded doubling dimension

Doubling Dimension, Embedding, NN Search

• Assouad showed: the snowflake of a doubling metric can be embedded in Euclidean space [A83]
  • ...and many embedding results since
• NN search data structures for bounded doubling dimension `d_A(U)`
  [C99] [KL04] [H-PM05] [Cole-G06]
  • Exponential in (only) `d_A`
  • Some are dependent (polylog) on the spread `\Delta` $$\Delta\equiv \frac{\max_{p,p'\in S} D(p,p')}{\min_{p,p'\in S, p\ne p'} D(p,p')}$$
    • AKA distance ratio, aspect ratio

Doubling Dimension and Approximate NN

• Reprise: the divide-and-conquer approach
• Universe `U`, distance `D`, sites `S \subset U`,
  `\diam\, S\equiv \max_{p,p'\in S} D(p,p') = 1`
• The general idea:
  • Pick `\delta \le 1`, find `\delta^2`-net `N \subset S`
  • Recursively build data structure,
    for each `B_p \equiv B(p, 3\delta)\cap S`, `p \in N`
  • To search: given `q`, find nearest `p \in N`; recursively search `B_p`
• (For no good reason, a changed of notation `S_p\rightarrow B_p`)

Approximate NN Search, Analysis

• Suppose `\delta \le 1/12`
  • `B_p` has radius at most `1/4`
  • At recursion depth `t`, radius is at most `4^{-t}`
  • Depth is at most `\log_2\Delta`
• Suppose `Z=(U,D)` has doubling dimension `d_A`
• Then `|N| = O(\delta^{-2d_A})`
  • ...as do all nets computed recursively, `\delta` scaling by ball radius
• Query time is `O(|N|\log\Delta) = O(12^{2d_A}\log\Delta)`
• All these bounds can be improved

Divide-and-Conquer

• "Divide-and-conquer" reprise:
  • Data structure `T(S)` is `N\subset S`, together with `T(B_p)`, for each `p\in N`
    • `B_p` a ball of appropriate radius, centered at `p`
  • For query `q`, to use `T(S)`: find NN of `q` in `p`, recursively search `T(S_p)`
• Above: approximate answers, `N` an `\epsilon`-net, bounded doubling dimension
  • Divide into smaller problems: `B_p` radius is smaller than half the radius of `S`
  • A crude version of [KL04]
• Next: exact queries w.h.p., `N` a random subset, doubling measures
  • Divide into smaller problems: `|B_p|\le \frac{1}{2}|S|`
  • A crude version of [KR02]

Doubling Measures

• `Z=(U,D,\mu)` is a doubling measure space if there is some `d_M = d_M(Z)` so that, for all `p\in U` and `r > 0`, $$\mu(B(p,r))\le 2^{d_M} \mu(B(p,r/2))$$
• For discrete spaces:
  `|B(p,r)| \le 2^{d_M} | B(p,r/2)|` when `|B(p,r/2)|` is large enough
• Put another way: the measure changes slowly, at all scales
• Doubling metric measure spaces have bounded doubling dimension
• Subsets of discrete spaces do not inherit doubling measure
  • However, random subsets do, roughly

Divide-and-Conquer for Doubling Measures

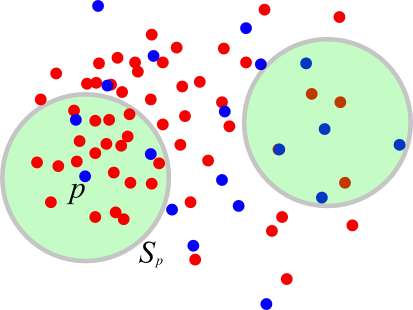
• Fix query point `q`, then choose random `N`,
  where `p\in S` chosen for `N` with probability `\frac{m}{n}`
  • `n=|S|`
  • `m` a parameter TBD
  • So `\E[|N|] = m`
• For `p\in N`, choose `r_p` so that `B_p \equiv B(p,r_p)` contains `4^{d_M}M` sites
  • `M\equiv K\frac{n}{m}\log n`
  • `K` is a large enough constant

Doubling Measures: `B_p` is Enough

• Suppose `D(p,q) < r_p/2`
  • From `p\overunder{\le r_p/2}{N}{\longleftarrow} q \overunder{\le r_p/2}{S}{\longrightarrow} a`, answer is in `B_p`
• Suppose `D(p,q) \ge r_p/2`
  
  • Then `B(p, r_p) \subset B(p, 2D(p,q))\subset 3B_q`,
    so `|3B_q| \ge 4^{d_M}M`
  • By doubling measure assumption, if `|3B_q| \ge 4^{d_M}M`, then `|B_q| \ge M`
  • But `|B_q| \ge M` implies:
    Chance that `B_q\cap N=\{\}` is `\le (1-m/n)^M \le 1/n^K`
  • So `p\overunder{}{N}{\longrightarrow} q` is very unlikely

Divide-and-Conquer

• First: approximate answers, `N` an `\epsilon`-net, bounded doubling dimension,
  • Divide into smaller problems: `B_p` radius is smaller than `\frac{1}{2}\diam S`
  • A crude version of [KL04]
• Second: exact queries w.h.p., `N` a random subset, doubling measures
  • Divide into smaller problems: `m` subproblems of size at most `O(2^{O(d_M)}\frac{n}{m}\log n)`
  • A crude version of [KR02]
• Next: exact queries w.h.p., `N` a random subset, bounded doubling dimension with exchangeable queries
  • Divide into smaller problems: `|B_p| \le \frac{1}{2}|S|`
  • A crude version of [C99]

Exchangeable Queries

• Exchangeable means: the queries "look like" the sites
  • For example: queries and sites i.i.d. with the same unknown distribution
  • Or: queries and sites random samples of a discrete set
  • Holds for NN classification, `k`-NN search, roughly for vector quantization
  • In experiments, test queries often chosen from hold-out subset of sites
• Claim: for random `N` with `m` sites, there are balls `B_p` for `p\in N` such that:
  `B_p\ni a \overunder{}{S}{\longleftarrow} q\overunder{}{N}{\longrightarrow} p`, and
  `|B_p| \le 2^{O(d_A)} \frac{n}{m}\log^2\Delta`, with high probability

Exchangeable Queries, Hints: (3)-NNs

• Since sites and queries have the same distribution,
  average behavior of queries = average for sites
• A site `p` is (3)-NN to a bounded number of other sites
  • `p` is a `(\gamma)`-NN to `p'` if `D(p,p')\le \gamma D(p',S)`
  
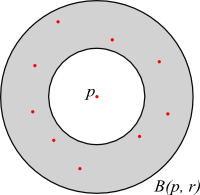
  • In `B(p,r)`, at most `2^{3d_A}` sites are farther than `r/6` from all others in `B(p,r)`, by the sphere-packing condition
  • So in annulus `B(p,r)\setminus B(p,r/2)`,
    `2^{3d_A}` sites `p'` that can have `p` as `(3)`-NN in `S`
  • So `p` is `(3)`-NN to at most `2^{O(d_A)}\log\Delta` sites

Exchangeable Queries, Hints: Dominating Queries

• So average `p\in S` has about `2^{O(d_A)}\log\Delta` (3)-NN's
• Why is this helpful?

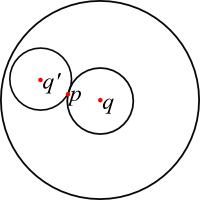
• For queries `q,q'`, if `q\overunder{v}{N}{\longrightarrow} p \overunder{\le v}{N}{\longleftarrow} q' \overunder{\le v}{S}{\longrightarrow} a`
  then `D(q,a)\le 3D(q,p)`
• So: in any collection `Q_p` of queries with `p` an NN in `N`,
  there is some `q\in Q_p` so that `B(q, 3D(q,p))` contains all answers for queries in `Q_p`
• Also: if that `q` behaves like an average `p\in S`, then `|B(q,3D(q,p))|` is bounded

Less Space

• So far, for simplicity, divide-and-conquer:
  • Data structure `T(S)` is `N` and collection of `T(B_p)`
  • To answer queries:
    1. Find `p\overunder{}{N}{\longleftarrow} q`
    2. Return `a \overunder{}{B_p}{\longleftarrow} q` found using `T(B_p)`
  • Crude, since `\sum_{p\in N} |B_p| \gg |S|`
• Better: make `|N|` large enough that `B_p` is constantly small, use `T(N)` for finding `p`
• Equivalently: a hierarchy of nested subsets `N_0 \subset N_1\subset N_2\subset\ldots\subset N_h=S`
  • Find NN in `N_{i-1}`, use to find NN in `N_i`

Less Space: Preprocessing

• New problem: how to find all `B_p` for `p\in N` for large `|N|`?
• Generically:
  • For `p'\in N_i`, track its NN in `N_j` for `j < i`
  • Use cross-links among sites in `N_i` to find `B_p` for `p\in N_{i-1}` containing `p'`

Less Space: Examples

• [H-PM05]
  • Bounded `d_A`, each `N_i` is (roughly) an `\epsilon^i`-net
  • Updating NN of `p` involves points of `\epsilon^i`-net in ball of radius `O(\epsilon^{i-1})`
  • Also, use ring separators to avoid dependence on spread
• Or:
  • `N_i` is a random subset, doubling dimension [C99][C03]
  • `N_i` is an `\epsilon^i`-net, use doubling measure to avoid dependence on spread [BKL04]
  • `N_i` is a union of skiplist levels, doubling measure [HKMR04]

Voronoi Grouping

• Even with more careful constructions, storage for trees based on DC is still exponential in `d_*`
  • And so fail one of the goals of a good generic NN data structure
  • Queries follow only one path to a leaf
  • That is, sites in `N_i` are grouped according to NN in `N_{i-1}`
• The "Voronoi grouping" trick technique:
  • Group sites according to NN in `N_i`:
    `V_p(i)\equiv \{p'\in S \mid p'\overunder{}{N_i\setminus\{p'\} }{\longrightarrow} p\}`
  • For increasing `i`, track all `p\in N_i` such that `V_p(i)` might contain answer to query

Voronoi Grouping: Ruling Out

• If `N` is an `\epsilon`-net, then
  `p \overunder{\le \epsilon}{N}{\longleftarrow} q \overunder{}{S}{\longrightarrow} a `
• Since `a` is NN in `S`,
  `p \overunder{\le\epsilon}{N}{\longleftarrow} q \overunder{\le \epsilon}{S}{\longrightarrow} a `
• Since `N` is an `\epsilon`-net,
  `p \overunder{\le\epsilon}{N}{\longleftarrow} q \overunder{\le \epsilon}{S}{\longrightarrow} a \overunder{\le \epsilon}{N}{\longrightarrow} p'`
• So if `D(p,p') > 3\epsilon`, then `V_{p'}` does not contain the NN to `q`
• More generally,
  `p \overunder{x}{N}{\longleftarrow} q \overunder{}{S}{\longrightarrow} a `
• Since `a` is NN in `S`,
  `p \overunder{x}{N}{\longleftarrow} q \overunder{\le x}{S}{\longrightarrow} a `
• Since `p'` is closest in `N`,
  `p \overunder{x}{N}{\longleftarrow} q \overunder{\le x}{S}{\longrightarrow} a \overunder{\le 2x}{N}{\longrightarrow} p'`
• So if `D(p,p') > 4 D(q,p)`, then `V_{p'}` does not contain the NN to `q`
  • Or if `D(q,p') > 3 D(q,p)`

Voronoi Grouping: An Example

• A data structure with cheap heuristic version [C99]
  • Pick random subset `N`, build `T(N)`
  • Build `T(V_p)` for each `p\in N`
  • Sum of `|V_p|` is `\le |S|`, so small space
• To answer queries:
  • Using `T(N)`, find `p\overunder{}{N}{\longleftarrow} q`
  • For each `p'\in N` with `D(p,p')\le 4 D(q,p)` and `D(q,p') \le 3 D(q,p)`,
    search `T(V_{p'})`, take the closest to `q` of all returned
• Almost analyzable for exchangeable queries, bounded `d_A`
  • Sites in `V_p` restricted in a way queries are not, breaking exchangeability
  • Solution: build `T(W_p)` recursively, where `W_p\supset V_p` preserves exchangeability

Voronoi Grouping: Other Work

Implementations only:
• Large `N`, Euclidean only [FN75]
• Bisector trees, `|N|=2` [KM83]
  • With no backtracking, used for vector quantization
• GNAT [Bri95]: `N` is an `\epsilon`-net of a random sample
• `sb` data structure [C03]
• Bounds:
  • `N_i` is a union of skiplist levels, doubling measure [HKMR04]
  • Cover trees: approximate, `O(n)` space, `\epsilon`-net hierarchy, doubling measure, implementation [BKL04]
  • approximate, `O(n)` space, `\epsilon`-net hierarchy, doubling dim, supports insert/delete [Cole-G06]

Barriers to Use in Practice

• Why aren't these nice, easy-to-use data structures used more? Maybe because:
  • Too complicated?
    • Shouldn't be a problem, if someone else has done the work
• Too slow?
  • A fix might be: open up the black box a little, use fast and cheap distance approximations when available

Thanks for Your Attention!

We got this Far?

Neighbors

• For `p,q \in U`, when is `p` a neighbor of `q`?
  If `D(q,p)` is bounded by:
  • `\epsilon` for a parameter `\epsilon` ` \implies \epsilon`-Rips neighbor
  • `D_k(q, U)` ` => k`-nearest neighbor
  • `\gamma D(q,U)` for a parameter `\gamma \ge 1` ` \implies (\gamma)`-near neighbor
• Surface reconstruction and data analysis
  • all-`k`-NN
  • But also: all-`(\gamma)`-near [GW03]
  • All-`(\gamma)`-near neighbors in spaces of bounded doubling dimension can be found in `\tilde{O}(n)` time [C99] [H-PM05] [IN07]

Weak Neighbors

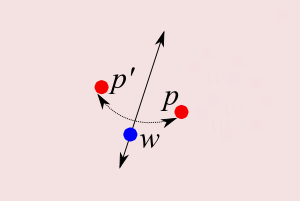
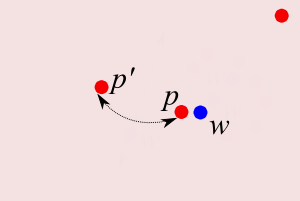
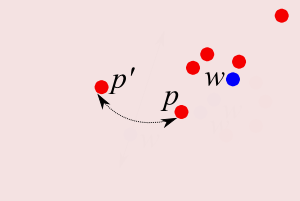
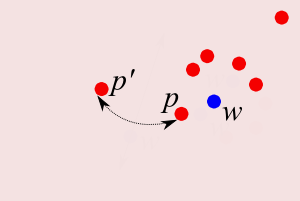
• Let:
  • `L\subset U` be landmarks
  • `W\subset U` be witnesses
  • `p,p'\in L`, `w\in W`
• `p\overunder{}{L}{\longleftarrow} w \overunder{}{L}{\longrightarrow} p'`: Delaunay neighbors
• `p\overunder{}{L}{\longleftarrow} w \overunder{}{2-L}{\longrightarrow} p'` : weak Delaunay [MS93] [dSC04]
• `p\overunder{}{k-L}{\longleftarrow} w \overunder{}{k-L}{\longrightarrow} p'` : `k`-weak Delaunay [GO08]
• `p\overunder{}{L}{\longleftarrow} w \overunder{\le \gamma D(w,L)}{}{\longrightarrow} p'` : `(\gamma)`-weak Delaunay neighbors [C99]

Neighborhoods: Analysis

• For `\epsilon`-Rips, `m/|L|^2 \approx \epsilon^{d_C}`, where `d_C` is the correlation dimension
• As studied in dynamical systems
• For weak neighbors:
• Each `w \in W` results in one pair, so `O(|W|)`
• For `(\gamma)`-weak neighbors, when `U` has bounded doubling dimension:
• For `L` an `\epsilon`-net, at most `\tilde{O}(1)` `p \in L` can be `(\gamma)`-near to a given `w \in W`, so `\tilde{O}(|W|)`
• For `L` and `W` random subsets of `U`, expected `\tilde{O}(|L|)` [C99]

Interpolation in Metric Spaces

• Interpolation: given `S \subset U`, and function values `f(x), x \in S`, estimate `\hat{f}(y)` for some `y \in U`
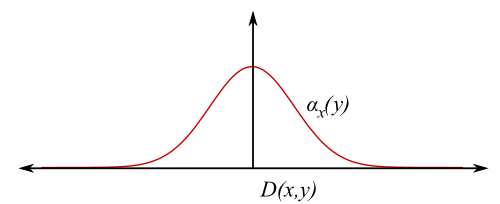
• Often `\hat{f}(y) \equiv \sum_{x \in S} \alpha_x(y) f(x)` , a weighted linear combination of the data values. Often:
• `\alpha_x(y) \ge 0`
• `\sum_{x \in S} \alpha_x(y) = 1` for all `y \in U`
• Possibly after normalizing by `\sum_{x \in S} \alpha_x(y)`
• If `y = \sum_{x \in S} \alpha_y(x) x`, then this scheme preserves linear functions
• What weights make sense in a metric space?

(The Laplacian as Interpolation)

• For `x \in S`, apply a scheme to `S \setminus \{x\}`, and compute `\hat{f}(x)`; then
  `\Delta f(x) \equiv f(x) - \hat{f}(x)`
  is a discrete Laplacian

Interpolation in Metric Spaces: Radial Functions

• One approach: `\alpha_x(y) = \exp(-D(x,y)^2)`
  • For point clouds, resulting Laplacian converges to Laplace-Beltrami operator [BN05]
• Radial functions
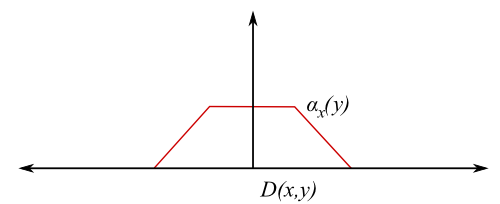
  • `S` an `\epsilon`-net, `\alpha_x(y)` is based on `D(y, S \setminus B(x,\epsilon))`
  • `\alpha_x(y) \equiv 1` close to `x`, tapers to zero away from `x`
• Both approaches involve a somewhat arbitrary choice of scale